All ACT Math Resources
Example Questions
Example Question #5 : How To Find A Missing Side With Cosine
In a given right triangle 




In right triangles, SOHCAHTOA tells us that 




Thus, 
Example Question #1 : How To Find A Missing Side With Cosine
In a given right triangle 




In right triangles, SOHCAHTOA tells us that 




Thus, 
Example Question #7 : How To Find A Missing Side With Cosine
An airline pilot must know the exact vertical height of his plane above the runway to know when to extend the landing gear under the nose. If the nose of the plane is 


(Ignore the height of the plane itself).
The plane itself is effectively at the top of a right triangle, with topmost angle 


Now, solve for the adjacent:
Thus, our plane's nose is approximately 
Example Question #8 : How To Find A Missing Side With Cosine
Edgar is standing at the top of a 35-foot long slide. He knows that the angle between the top of the slide and the ladder that he climbed to reach the top is 68 degrees. If the ladder meets the ground at a right angle, how far did Edgar climb?
Edgar is standing on top of a right triangle because the angle from the vertical ladder to the ground is 90 degrees. To solve this question, you must know SOHCAHTOA. This acronym can be broken into three parts to solve for the sine, cosine, and tangent.
In order to solve for the missing side, you need to choose the trigonometric function that includes the side you need to find and the side that you know, relative to the angle that you know. In this case, you know the hypotenuse, so you would not use the tangent function; furthermore, you are looking for the side that is adjacent to the 68-degree angle. Thus, you need the function that incorporates adjacent and hypotenuse—the cosine function.
Typically, you would use a calculator at this point to calculate the cosine function; however, based on the answer choices provided, you can stop at this point.
Example Question #11 : Cosine
In a given right triangle 




In right triangles, SOHCAHTOA tells us that 


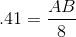

Thus, 
Example Question #11 : Cosine
What is the domain of 
Does not exist.
The domain of a function is referring to the x values that can be plugged into the function and produce a value.
The domain of the parent function 
The 
Therefore, the answer is 
Example Question #111 : Trigonometry
Given a function 
The function 

The domain of the parent function is 


The answer is 
Example Question #3031 : Act Math
What is the domain of the following trigonometric equation:
For sine and cosine, they can take any for 
Example Question #4 : How To Find The Domain Of The Cosine
What is the domain of the function 
The domain of a function refers to all possible values of 





Example Question #2 : How To Find The Domain Of The Cosine
What is the domain of the function 
The domain of a function refers to all possible values of 





Note that adding 

Certified Tutor
All ACT Math Resources
































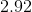



![(-\infty,-3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/303613/gif.latex)

![[-3,3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/303611/gif.latex)

![[2,6]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/315532/gif.latex)





![[-2\pi,2\pi]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/432610/gif.latex)
![[-2,2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/432607/gif.latex)
![[-12,12]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/432608/gif.latex)

![[2,12]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/432609/gif.latex)


![(-\infty, 1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/548086/gif.latex)
![[-\pi, \pi]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/548089/gif.latex)

![[-1, 1]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/548088/gif.latex)
![[-7, 7]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/548094/gif.latex)



![(-\infty, 7]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/548091/gif.latex)



