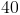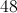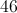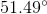ACT Math : How to find the tangent for the missing side
Study concepts, example questions & explanations for ACT Math
All ACT Math Resources
Example Questions
Example Question #12 : Trigonometry
What is the perimeter of the following figure?
The question asks for you to find the perimeter of the given figure. The figure has twelve sides total, of two varying lengths. One length is given to you, 4. The other length must be solved for using either the sine or tangent functions. However, one can arrive to answer more quickly by recognizing that the drawn triangle is actually a 3-4-5 triangle, where 3, 4, and 5 corresponds to each of the sides of the triangle. This is a pythagorean triple and this ratio should be easily remembered.
Thus if 3 is the missing side, and there are eight sides of length 3 and four sides of length 4, one can arrive to the answer:
Example Question #1 : How To Find The Tangent For The Missing Side
A man is setting up a laser on the ground, angling it toward the very top of a flag pole. If the flag pole is 
You can draw out your scenario like a triangle:
Now, you know that this means:
Using your calculator, you can utilize the inverse 
This rounds to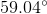 
Example Question #2 : How To Find The Tangent For The Missing Side
For the right triangle shown below, what is the value of
To solve this question, you must know SOHCAHTOA. This acronym can be broken into three parts to solve for the sine, cosine, and tangent.
We can use this information to solve our identity.
Dividing by a fraction is the same as multiplying by its reciprocal.
The sine divided by cosine is the tangent of the angle.
All ACT Math Resources
