All ACT Math Resources
Example Questions
Example Question #3 : How To Find The Length Of An Edge
A tetrahedron has a volume that is twice the surface area times the edge. What is the length of the edge? (In the answer choices, 
The problem states that the volume is:
The point of the problem is to solve for the length of the edge. Becasuse there are no numbers, the final answer will be an expression.
In order to solve for it, we will have to rearrange the formula for volume in terms of 
Example Question #1 : Tetrahedrons
Calculate the diagonal of a regular tetrahedron (all of the faces are equilateral triangles) with side length 
The diagonal of a shape is simply the length from a vertex to the center of the face or vertex opposite to it. With a regular tetrahedron, we have a face opposite to the vertex, and this basically amounts to calculating the height of our shape.
We know that the height of a tetrahedron is 

which gives us the correct answer.
Example Question #1 : How To Find The Surface Area Of A Tetrahedron
If the edge length of a tetrahedron is 
Write the formula for finding the surface area of a tetrahedron.
Substitute the edge and solve.
Example Question #81 : Solid Geometry
Each of the faces of a regular tetrahedron has a base of 

The surface area is the area of all of the faces of the tetrahedron. To begin, we must find the area of one of the faces. Because a tetrahedron is made up of triangles, we simply plug the given values for base and height into the formula for the area of a triangle:
Therefore, the area of one of the faces of the tetrahedron is 
Therefore, the surface area of the tetrahedron is 
Example Question #3 : Tetrahedrons
What is the surface area of a regular tetrahedron with a slant height of 
Cannot be determined
If this is a regular tetrahedron, then all four triangles are equilateral triangles.
If the slant height is 

In order to solve for the surface area, we can use the formula
where 
The problem has not given the edge; however, it has provided information that will allow us to solve for the edge and therefore the surface area.
Picture an equilateral triangle with a height 
Drawing in the height will divide the equilateral triangle into two 30/60/90 right triangles. Because this is an equilateral triangle, we can deduce that finding the measure of the hypotenuse will suffice to solve for the edge length (
In order to solve for the hypotenuse of one of the right triangles, either trig functions or the rules of the special 30/60/90 triangle can be used.
Using trig functions, one option is using 
Rearranging the equation to solve for 
Now that 
Example Question #13 : How To Find The Surface Area Of A Tetrahedron
What is the surface area of a regular tetrahedron when its volume is 27?
The problem is essentially asking us to go from a three-dimensional measurement to a two-dimensional one. In order to approach the problem, it's helpful to see how volume and surface area are related.
This can be done by comparing the formulas for surface area and volume:

We can see that both calculation revolve around the edge length.
That means, if we can solve for 
Now that we know 
Example Question #12 : How To Find The Volume Of A Tetrahedron
Find the volume of a regular tetrahedron if one of its edges is ![\sqrt[3]{6}\:cm](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/301892/gif.latex)
Write the volume equation for a tetrahedron.
In this formula, 

Substitute the given edge length and solve.
Rationalize the denominator.
Example Question #12 : Volume
Find the volume of a tetrahedron if the side length is 
Write the equation to find the volume of a tetrahedron.
Substitute the side length and solve for the volume.
Rationalize the denominator.
Example Question #13 : How To Find The Volume Of A Tetrahedron
What is the volume of a regular tetrahedron with an edge length of 6?
The volume of a tetrahedron can be solved for by using the equation:
where 
This problem can be quickly solved by substituting 6 in for 
Example Question #1 : How To Find The Radius Of A Sphere
The surface area of a sphere is 
Solve the equaiton for the surface area of a sphere for the radius and plug in the values:
Certified Tutor
Certified Tutor
All ACT Math Resources


![a= \sqrt[3]{\frac{V}{2\sqrt{3}}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/376802/gif.latex)

![a= \sqrt[4]{\frac{V}{\sqrt{3a^2}}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/376806/gif.latex)
![a= \sqrt[3]{\frac{V}{2\sqrt a^2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/376804/gif.latex)



![a= \sqrt[3]{\frac{V}{2\sqrt3}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/376810/gif.latex)




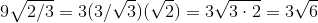





































![\sqrt[3]{27 \cdot 6\sqrt{2}}=a](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/376629/gif.latex)










![V=\frac{(\sqrt[3]6\:cm)^3}{6\sqrt2} = \frac{6\:cm^3}{6\sqrt2}= \frac{1}{\sqrt2}\:cm](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/301896/gif.latex)

























