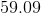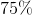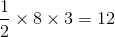To solve this question, you need to remember that the sum of the angles in a triangle is 180°. You also need to remember supplementary angles. If you know what ∠ DCE is, you also know what ∠ ECA is. Hence you know two angles of the triangle, 180°-80°-50°= 50°. 

The measure of \(\displaystyle \dpi{100} \small \angle ADB\) is \(\displaystyle 30^{\circ}\). Since \(\displaystyle \dpi{100} \small A\), \(\displaystyle \dpi{100} \small B\), and \(\displaystyle \dpi{100} \small C\) are collinear, and the measure of \(\displaystyle \dpi{100} \small \angle CBD\) is \(\displaystyle 60^{\circ}\), we know that the measure of \(\displaystyle \dpi{100} \small \angle ABD\) is \(\displaystyle 120^{\circ}\).

Because the measures of the three angles in a triangle must add up to \(\displaystyle 180^{\circ}\), and two of the angles in triangle \(\displaystyle \dpi{100} \small ABD\) are \(\displaystyle 30^{\circ}\) and \(\displaystyle 120^{\circ}\), the third angle, \(\displaystyle \dpi{100} \small \angle ADB\), is \(\displaystyle 30^{\circ}\).

Two triangles are only congruent if all of their sides are the same length, and all of the corresponding angles are of the same degree. Luckily, we only need three of these six numbers to completely determine the others, as long as we have at least one angle and one side, and any other combination of the other numbers.

In this case, we have two adjacent angles and one side, directly across from one of our angles in both triangles. This can be called the AAS case. We can see from our picture that all of our angles match, and the two sides match as well. They're all in the same position relative to each other on the triangle, so that is enough information to say that the two triangles are congruent.

Adding the sides gives a perimeter of 15 for the smaller triangle. Multipying by the given ratio of \(\displaystyle \frac{7}{2}\), yields 52.5.

The larger triangle has a perimeter of 25 inches. Therefore, using a 4:5 ratio, the smaller triangle's perimeter will be 20 inches.

1. Find the perimeter of the larger triangle:

\(\displaystyle 14+18+24=56\)

2. Use the given ratio to find the perimeter of the smaller triangle:

\(\displaystyle \frac{2}{5}=\frac{x}{56}\)

Cross multiply and solve:

\(\displaystyle (2)(56)=5x\)

\(\displaystyle \frac{112}{5}=x=22.4\)

Use proportions to solve for the perimeter of the larger triangle:

\(\displaystyle \frac{7}{9}=\frac{16.8}{x}\)

Cross multiply and solve:

\(\displaystyle (9)(16.8)=7x\)

\(\displaystyle \frac{151.2}{7}=x=21.6\)

Since the perimeter of the smaller triangle is \(\displaystyle 3m + 4m + 5m = 12m\), and since the larger triangle has a perimeter in the \(\displaystyle 4:5\) ratio, we can set up the following identity, where \(\displaystyle x=\) the perimeter of the larger triangle:

\(\displaystyle \frac{12}{x} = \frac{4}5{}\)

In cross multiplying this identity, we get \(\displaystyle 4x = 60\). We can now solve for \(\displaystyle x\). Here, \(\displaystyle x=15\), so the perimeter of the larger triangle is \(\displaystyle 15m\).

Begin by filling in the missing angle for your triangle. Since a triangle has a total of \(\displaystyle 180\) degrees, you know that the missing angle is:

\(\displaystyle 180-50-30=100\)

Draw out the figure:

Now, to solve this, you will need some trigonometry. Use the Law of Sines to calculate the value:

\(\displaystyle \frac{sin(30)}{30}=\frac{sin(100)}{x}\)

Solving for \(\displaystyle x\), you get:

\(\displaystyle x=\frac{30sin(100)}{sin(30)}=59.0884651807326...\)

Rounding, this is \(\displaystyle 59.09\).

The formula for the area of a triangle is

 \(\displaystyle \frac{1}{2}b \times h\) .

If the area is equal to 48 cm² and the base is 8 cm, then the initial height is: 

\(\displaystyle 48 = \frac{1}{2} \times 8 \times h\)

\(\displaystyle h = 12\)

If 12 is decreased by 75% then

\(\displaystyle 12 \times .75 = 9\), and \(\displaystyle 12 - 9 =3\). The final height is 3 cm.

Therefore the final area is

\(\displaystyle \frac{1}{2}\times 8\times 3=12\).