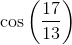All ACT Math Resources
Example Questions
Example Question #3 : How To Find The Area Of A Hexagon

The figure above is a regular hexagon. 
What is the area of the figure above?
You can redraw the figure given to notice the little equilateral triangle that is formed within the hexagon. Since a hexagon can have the 



Now, the 




We know, then, that:
Another way to write 
Now, there are several ways you could proceed from here. Notice that there are 
and for your data...
The area of the whole figure is:

Example Question #4 : How To Find The Area Of A Hexagon
What is the area of a regular hexagon with a perimeter of 
A hexagon has 


This question is asking about the area of a regular hexagon that looks like this:

Now, you could proceed by noticing that the hexagon can be divided into little equilateral triangles:

By use of the properties of isosceles and 




It is likely easiest merely to memorize the aforementioned equation for the area of an equilateral triangle. From this, you can derive the hexagon area equation mentioned above. Using this equation and our data, we know:
Example Question #5 : How To Find The Area Of A Hexagon
What is the area of a regular hexagon with a side length of 


For a hexagon with side length 

We have a side length of 4 miles, so we plug that into the equation and simplify the fraction.
Example Question #1 : How To Find The Area Of A Hexagon
What is the area of a hexagon with a side of length two? Simplify all fractions and square roots.
To find the area of a hexagon with a given side length, 
Plugging in 2 for 

Example Question #901 : Plane Geometry
A single hexagonal cell of a honeycomb is two centimeters in diameter.

What’s the area of the cell to the nearest tenth of a centimeter?
Cannot be determined
How do you find the area of a hexagon?
There are several ways to find the area of a hexagon.
- In a regular hexagon, split the figure into triangles.
- Find the area of one triangle.
- Multiply this value by six.
Alternatively, the area can be found by calculating one-half of the side length times the apothem.
Regular hexagons:
Regular hexagons are interesting polygons. Hexagons are six sided figures and possess the following shape:
In a regular hexagon, all sides equal the same length and all interior angles have the same measure; therefore, we can write the following expression.

One of the easiest methods that can be used to find the area of a polygon is to split the figure into triangles. Let's start by splitting the hexagon into six triangles.

In this figure, the center point, 


We also know the following:
Now, let's look at each of the triangles in the hexagon. We know that each triangle has two two sides that are equal; therefore, each of the base angles of each triangle must be the same. We know that a triangle has 
Each angle in the triangle equals 



Let's solve for the length of this triangle. Remember that in 
Now, we can analyze 


We know the measure of both the base and height of 
Now, we need to multiply this by six in order to find the area of the entire hexagon.
We have solved for the area of a regular hexagon with side length, 
If we are not given a regular hexagon, then we an solve for the area of the hexagon by using the side length(i.e. 



Alternative method:
If we are given the variables 

In this equation, 




Solution:
In the problem we are told that the honeycomb is two centimeters in diameter. In order to solve the problem we need to divide the diameter by two. This is because the radius of this diameter equals the interior side length of the equilateral triangles in the honeycomb. Lets find the side length of the regular hexagon/honeycomb.
Substitute and solve.
We know the following information.
As a result, we can write the following:
Let's substitute this value into the area formula for a regular hexagon and solve.
Simplify.
Solve.
Round to the nearest tenth of a centimeter.
Example Question #52 : Geometry
Two hexagons are similar. If they have the ratio of 4:5, and the side of the first hexagon is 16, what is the side of the second hexagon?
This type of problem can be solved through using the formula:
If the ratio of the hexagons is 4:5, then 


Substituting in the numbers, the formula looks like:
This quickly begins a problem where the second area can be solved for by rearranging all the given information.
The radical can then by simplified with or without a calculator.
Without a calculator, the 320 can be factored out and simplified:

Example Question #21 : Hexagons
The ratio between two similar hexagons is 

This kind of problem can be solved for by using the formula:
where the 

In this case, the problem provides 



There are four variables in this formula, and three of them are provided in the problem. This means that we can solve for 


Example Question #51 : Act Math
The measure of 3 angles in a triangle are in a 1:2:3 ratio. What is the measure of the middle angle?
The angles in a triangle sum to 180 degrees. This makes the middle angle 60 degrees.
Example Question #1 : How To Find An Angle In A Right Triangle
A 17 ft ladder is propped against a 15 ft wall. What is the degree measurement between the ladder and the ground?
Since all the answer choices are in trigonometric form, we know we must not necessarily solve for the exact value (although we can do that and calculate each choice to see if it matches). The first step is to determine the length of the ground between the bottom of the ladder and the wall via the Pythagorean Theorem: "x2 + 152 = 172"; x = 8. Using trigonometric definitions, we know that "opposite/adjecent = tan(theta)"; since we have both values of the sides (opp = 15 and adj = 8), we can plug into the tangential form tan(theta) = 15/8. However, since we are solving for theta, we must take the inverse tangent of the left side, "tan-1". Thus, our final answer is
Example Question #1 : Triangles
What is the sine of the angle between the base and the hypotenuse of a right triangle with a base of 4 and a height of 3?
By rule, this is a 3-4-5 right triangle. Sine = (the opposite leg)/(the hypotenuse). This gives us 3/5.
All ACT Math Resources














































![\textup{Area of Hexagon}[ABCDEF]=6\times\frac{\sqrt{3}s^2}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065143/gif.latex)
![\textup{Area of Hexagon}[ABCDEF]=\frac{6 \sqrt{3}s^2}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065144/gif.latex)
![\textup{Area of Hexagon}[ABCDEF]=\frac{3\sqrt{3}}{2}\times s^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065145/gif.latex)