All ACT Math Resources
Example Questions
Example Question #1 : How To Find The Intersection Of A Venn Diagram
Students at a local high school are given the option to take one gym class, one music class or one of each. Out of 100 students, 60 say that they are currently taking a gym class and 70 say that they are taking a music class. How many students are taking both?
This problem can be solved two ways, with a formula or with reason.
Using the formula, the intersection of the Venn diagram for which classes students take is:
By using reason, it is clear that 60 + 70 is greater than 100 by 30. It is assumed that this extra 30 students come from students who were counted twice because they took both classes.
Example Question #1 : How To Find The Intersection Of A Venn Diagram
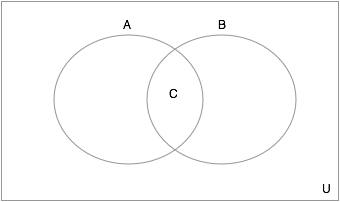
In the Venn Diagram shown above, let the set 





To find the intersection of a set of numbers, we need to find all numbers that are in both sets (definition of intersection). We can see that all the primes less than 

Example Question #5 : How To Find The Intersection Of A Venn Diagram

In the Venn Diagram shown above, let 











Since the universe is integers less than or equal to 10, we see that the only ones that fit that description that are not in 
Example Question #2942 : Sat Mathematics
There are 75 juniors at a high school. 15 of the students are enrolled in Physics and 40 students are enrolled in Chemistry. 30 students are not enrolled in either Physics or Chemistry. How many students are enrolled in both Physics and Chemistry?
15
30
10
5
25
10
First, subtract the students that are in neither class; 75 – 30 = 45 students.
Thus, 45 students are enrolled in Chemistry, Physics, or both. Of these 45 students, we know 40 are in Chemistry, so that leaves 5 students who are enrolled in Physics only; with 15 total students in Physics, that means 10 must be in Chemistry as well. So 10 students are in both Physics and Chemistry.
Example Question #1 : Statistics
Angela scores 17, 19, 13, 24, and 14 points in the first five games of a seven-game basketball season. If the scoring leader in Angela’s league averages 18 points per game, how many points must Angela score in the final two games combined to end the season with the highest scoring average in the league AND have a higher scoring average than any other player?
34
39
32
37
40
40
Since a given player’s scoring average can be determined by dividing the sum total of points scored by the number of games, we can determine the total points of the scoring leader by multiplying the average points per game by the total number of games. 18 x 7 = 126. Angela would have to score 1 more point than the current scoring leader. Angela’s current total is 87 points; therefore, she must score 40 (87 + 40 = 127) over the course of the final two games to have the highest average points per game in the league.
Example Question #12 : Data Analysis
What is the mean of the following set of numbers: 13, 15, 100, 54, 345, rounded to the nearest 1’s place?
105
100
106
135
105
mean = sum of all values divided by the number of values.
Example Question #11 : Data Analysis
The mean of five numbers is 40. The mean of the smallest two numbers is 25. What is the mean of the other three numbers?
60
55
40
50
45
50
The equation for the mean of a group of numbers is to find the sum of all of the numbers and then divide by how many numbers are in the group. This means that if we know the mean and how many numbers are in the group, we can find the sum of those numbers.
(sum of all five numbers) / 5 = 40 --> sum of all five numbers = 200
(sum of two smallest numbers) / 2 = 25 --> sum of two smallest numbers = 50
Subtracting the sum of the two smallest numbers from the sum of all five gives us the sum of the remaining three. We can then divide by three to find the mean of those three remaining numbers.
200 – 50 = 150
150 / 3 = 50
Example Question #2 : How To Find Arithmetic Mean
LeBron James had played in 7 playoff games. He scored 31, 30, 55, 14, 29, 20, and 12 points in those games. What is his average for those 7 games?
20.5 points
29 points
43 points
27.3 points
22 points
27.3 points
To find the mean, you have to add all of the items and then divide by the number of items. Finding the sum (31+30+55+14+29+20+12)= 191 and then dividing by 7 would give a result of 27.3. [Side Note: The Median is 29 and the range is 43.]
Example Question #1 : Statistics
Kobe Bryant has averaged about 29.5 points a game through the first 81 games of the NBA season. His goal is to average at least 30 points per game for the season. What is the least amount of points he needs to score in his last game of the season to achieve his goal? (There are 82 games in a season.)
51 points
41 points
61 points
31 points
71 points
71 points
To find your answer, you would have to set it up like a weighted average because we don’t know what he scored for the 81 games, but we can approximate how many actual points he scored by multiplying 29.5 times 81. Thus, we would get the equation (29.5(81)+x)/82=30. Multiply both sides by 82 to get 2389.5+x=2460. Thus x=70.5 and we would round up to get 71 points.
Example Question #1 : Arithmetic Mean
Peter received the following 4 grades on math tests: 86, 90, 88, and 96. What was Peter's average score for the 4 tests?
92
90
89
88
91
90
In order to calculate the average, or arithmetic mean, of numbers in a set, we add up all of the numbers, then divide that total sum by the n (the count of numbers in the set).
Here we have 86, 90, 88, and 96. This gives us n = 4.
We add up 86 + 90 + 88 + 96 = 360. 360 / 4 = 90.
All ACT Math Resources





























