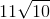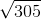All ACT Math Resources
Example Questions
Example Question #11 : How To Simplify Square Roots
Simplify the following square root:
The square root is already in simplest form.
The square root is already in simplest form.
We need to factor the number in the square root and find pairs of factors inorder to simplify a square root.
Since 83 is prime, it cannot be factored.
Thus the square root is already simplified.
Example Question #801 : New Sat
Right triangle 

If the triangle is a right triangle, then it follows the Pythagorean Theorem. Therefore:

At this point, factor out the greatest perfect square from our radical:
Simplify the perfect square, then repeat the process if necessary.
Since 
Example Question #802 : New Sat
Simplify:
There are two ways to solve this problem. If you happen to have it memorized that 


If you haven't memorized perfect squares that high, a fairly fast method can still be achieved by following the rule that any integer that ends in 

Now, we can use this rule again:
Remember that we multiply numbers that are factored out of a radical.
The last step is fairly obvious, as there is only one choice:
Example Question #803 : New Sat
Simplify:
A good method for simplifying square roots when you're not sure where to begin is to divide by 




As it turns out, 
Example Question #81 : Arithmetic
Simplify:
Again here, if no perfect square is easily recognized try dividing by 


Note that the 


Example Question #81 : Arithmetic
Simplify:
To solve, simply find a perfect square factor and pull it out of the square root.
Recall the factors of 48 include (16, 3). Also recall that 16 is a perfect square since 4*4=16.
Thus,
Example Question #812 : New Sat
Solve:
The trick to these problems is to simplify the radical by using the following rule: 


Example Question #11 : Simplifying Square Roots
Simplify:
When simplifying the square root of a number that may not have a whole number root, it's helpful to approach the problem by finding common factors of the number inside the radicand. In this case, the number is 24,300.
What are the factors of 24,300?
24,300 can be factored into:
When there are factors that appear twice, they may be pulled out of the radicand. For instance, 100 is a multiple of 24,300. When 100 is further factored, it is 
![10\sqrt[2]{243}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267786/gif.latex)
But 243 can also be factored:
Following the same principle as for the 100, the problem would become![9\cdot 10\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267789/gif.latex)
9 and 10 may be multiplied together, yielding the final simplified answer of
Example Question #3 : Arithmetic
To solve the equation 
When a factor appears twice, we can take it out of the square root.
Now the numbers can be added directly because the expressions under the square roots match.
Certified Tutor
All ACT Math Resources




















































![\sqrt[2]{24,300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267782/gif.latex)
![900\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267780/gif.latex)
![10\sqrt[2]{243}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267778/gif.latex)
![9\sqrt[2]{300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267781/gif.latex)
![90\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267774/gif.latex)
![90\sqrt[2]{270}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267776/gif.latex)
![\sqrt[2]{24,300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267783/gif.latex)
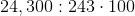


![90\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267790/gif.latex)