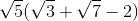Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Basic Squaring / Square Roots

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 Next →

Example Question #1 : How To Find The Common Factor Of Square Roots

$\sqrt{2016} + \sqrt{896} = ?$

Possible Answers:

$20\sqrt{14}$

75.0

$\sqrt{2919}$

54.0

$208\sqrt{14}$

Correct answer:

$20\sqrt{14}$

Explanation:

To solve the equation $\sqrt{2016} + \sqrt{896} = ?$ , we can first factor the numbers under the square roots.

$\sqrt{2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 3\cdot 3\cdot 7} + \sqrt{2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 7} = ?$

When a factor appears twice, we can take it out of the square root.

$2\cdot 2\cdot 3\sqrt{2\cdot 7} + 2\cdot 2\cdot 2\sqrt{2\cdot 7} = ?$

$12\sqrt{14} + 8 \sqrt{14} = ?$

Now the numbers can be added directly because the expressions under the square roots match.

$12\sqrt{14} + 8\sqrt{14} = 20\sqrt{14}$

Report an Error

Example Question #2 : How To Find The Common Factor Of Square Roots

Solve for .

$x\sqrt{96} + x\sqrt{150} = \sqrt{162}$

Possible Answers:

$9\sqrt{2}$

${\sqrt{3}}$

$\frac{1}{\sqrt{3}}$

$9\sqrt{12}$

$\frac{1}{\sqrt{6}}$

Correct answer:

$\frac{1}{\sqrt{3}}$

Explanation:

First, we can simplify the radicals by factoring.

$x\sqrt{96} + x\sqrt{150} = \sqrt{162}$

$x\sqrt{2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 3} + x\sqrt{2\cdot 3\cdot 5\cdot 5} = \sqrt{2\cdot 3\cdot 3\cdot 3\cdot 3}$

$x\left (2\cdot 2 \right )\sqrt{2\cdot 3} + x\left ( 5\right )\sqrt{2\cdot 3} = \left (3\cdot 3 \right )\sqrt{2}$

$4x\sqrt{6} + 5x\sqrt{6} = 9\sqrt{2}$

Now, we can factor out the .

$x\left (4\sqrt{6} + 5\sqrt{6} \right ) = 9\sqrt{2}$

$x\left (9\sqrt{6} \right ) = 9\sqrt{2}$

Now divide and simplify.

$x = \frac{9\sqrt{2}}{9\sqrt{6} } = \frac{\sqrt{2}}{\sqrt{2\cdot 3}} = \frac{1}{\sqrt{3}}$

Report an Error

Example Question #21 : Arithmetic

Which of the following is equivalent to:

$\sqrt{210}+\sqrt{55}$ ?

Possible Answers:

$5\sqrt{7}+\sqrt{11}$

$7\sqrt{30}+5\sqrt{11}$

$5\sqrt{462}$

$\sqrt{5}(\sqrt{42}+\sqrt{11})$

$\sqrt{265}$

Correct answer:

$\sqrt{5}(\sqrt{42}+\sqrt{11})$

Explanation:

To begin with, factor out the contents of the radicals. This will make answering much easier:

$\sqrt{210}+\sqrt{55}=\sqrt{2*3*5*7}+\sqrt{5*11}$

They both have a common factor . This means that you could rewrite your equation like this:

$\sqrt{5}\sqrt{2*3*7}+\sqrt{5}\sqrt{11}$

This is the same as:

$\sqrt{5}\sqrt{42}+\sqrt{5}\sqrt{11}$

These have a common $\sqrt{5}$ . Therefore, factor that out:

$\sqrt{5}\sqrt{42}+\sqrt{5}\sqrt{11}=\sqrt{5}(\sqrt{42}+\sqrt{11})$

Report an Error

Example Question #1 : How To Find The Common Factor Of Square Roots

Simplify:

$\sqrt{15}-\sqrt{20}+\sqrt{35}$

Possible Answers:

$\sqrt{5}(\sqrt{3}+\sqrt{7}-2)$

$\sqrt{7}-3\sqrt{5}$

$\sqrt{2}(\sqrt{5}+2\sqrt{7})$

$\sqrt{5}(\sqrt{10}-2)$

$2\sqrt{15}+\sqrt{2}$

Correct answer:

$\sqrt{5}(\sqrt{3}+\sqrt{7}-2)$

Explanation:

These three roots all have a in common; therefore, you can rewrite them:

$\sqrt{15}-\sqrt{20}+\sqrt{35}=\sqrt{3*5}-\sqrt{4*5}+\sqrt{7*5}$

Now, this could be rewritten:

$\sqrt{3*5}-\sqrt{4*5}+\sqrt{7*5}=\sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{4}+\sqrt{5}\sqrt{7}$

Now, note that $\sqrt{4}=2$

Therefore, you can simplify again:

$\sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{4}+\sqrt{5}\sqrt{7}=\sqrt{5}\sqrt{3}-2\sqrt{5}+\sqrt{5}\sqrt{7}$

Now, that looks messy! Still, if you look carefully, you see that all of your factors have $\sqrt{5}$ ; therefore, factor that out:

$\sqrt{5}\sqrt{3}-2\sqrt{5}+\sqrt{5}\sqrt{7}=\sqrt{5}(\sqrt{3}-2+\sqrt{7})$

This is the same as:

$\sqrt{5}(\sqrt{3}+\sqrt{7}-2)$

Report an Error

Example Question #1 : Factoring Common Factors Of Squares And Square Roots

Simplify:

$x\sqrt{50}+x\sqrt{8}-\sqrt{18}+\sqrt{98}$

Possible Answers:

22x

$11x\sqrt{2}$

$\sqrt{3}(5x-3)$

$\sqrt{2}(7x+4)$

$11x\sqrt{2}$

Correct answer:

$\sqrt{2}(7x+4)$

Explanation:

Begin by factoring out the relevant squared data:

$x\sqrt{50}+x\sqrt{8}-\sqrt{18}+\sqrt{98}$ is the same as

$x\sqrt{25*2}+x\sqrt{4*2}-\sqrt{9*2}+\sqrt{49*2}$

This can be simplified to:

$5x\sqrt{2}+2x\sqrt{2}-3\sqrt{2}+7\sqrt{2}$

Since your various factors contain square roots of , you can simplify:

$7x\sqrt{2}+4\sqrt{2}$

Technically, you can factor out a $\sqrt{2}$ :

$\sqrt{2}(7x+4)$

Report an Error

Example Question #4 : How To Find The Common Factor Of Square Roots

Solve for :

$t\sqrt{28}-t\sqrt{63}=\sqrt{14}$

Possible Answers:

$\sqrt{14}$

$-\sqrt{2}$

$-\sqrt{14}$

Correct answer:

$-\sqrt{2}$

Explanation:

Begin by breaking apart the square roots on the left side of the equation:

$t\sqrt{4*7}-t\sqrt{9*7}=\sqrt{14}$

This can be rewritten:

$2t\sqrt{7}-3t\sqrt{7}=\sqrt{14}$

You can combine like terms on the left side:

$-t\sqrt{7}=\sqrt{14}$

Solve by dividing both sides by $-\sqrt{7}$ :

$t=\frac{-\sqrt{14}}{\sqrt{7}}$

This simplifies to:

$t=-\sqrt{2}$

Report an Error

Example Question #5 : How To Find The Common Factor Of Square Roots

Solve for :

$x\sqrt{28} + x\sqrt{84} = 12$

Possible Answers:

$x = \frac{\sqrt{7}}{(\sqrt{7} +\sqrt{21})}$

$x = \frac{6}{(\sqrt{14} +\sqrt{21})}$

$x = \frac{12}{(\sqrt{7} +\sqrt{21})}$

$x = \frac{6}{(\sqrt{7} +\sqrt{21})}$

$x = \frac{6}{(\sqrt{7} -\sqrt{21})}$

Correct answer:

$x = \frac{6}{(\sqrt{7} +\sqrt{21})}$

Explanation:

To begin solving this problem, find the greatest common perfect square for all quantities under a radical.

$x\sqrt{28} + x\sqrt{84} = 12$ ---> $x\sqrt{4 \cdot 7} + x\sqrt{4 \cdot 21} = 12$

Pull out of each term on the left:

$x\sqrt{4 \cdot 7} + x\sqrt{4 \cdot 21} = 12$ ---> $2x\sqrt{7} + 2x\sqrt{21} = 12$

Next, factor out from the left-hand side:

$2x\sqrt{7} + 2x\sqrt{21} = 12$ ---> $2x(\sqrt{7} +\sqrt{21}) = 12$

Lastly, isolate :

$2x(\sqrt{7} +\sqrt{21}) = 12$ ---> $x = \frac{6}{(\sqrt{7} +\sqrt{21})}$

Report an Error

Example Question #1 : How To Find The Common Factor Of Square Roots

Solve for : $x\sqrt{125} + 5x\sqrt{70} = \sqrt{5}$

Possible Answers:

$x = \frac{5}{1+10\sqrt{3}}$

$x = \frac{3}{5+4\sqrt{3}}$

$x = \frac{5}{5\sqrt{12}}$

$x = \frac{5}{1+\sqrt{12}}$

$x = \frac{1}{5+10\sqrt{3}}$

Correct answer:

$x = \frac{1}{5+10\sqrt{3}}$

Explanation:

Solving this one is tricky. At first glance, we have no common perfect square to work with. But since each term can produce the quantity $\sqrt{5}$ , let's start there:

$x\sqrt{125} + 5x\sqrt{70} = \sqrt{5}$ ---> $x\sqrt{25 \cdot 5} + 5x\sqrt{12 \cdot 5} = \sqrt{5}$

Simplify the first term:

$x\sqrt{25 \cdot 5} + 5x\sqrt{12 \cdot 5} = \sqrt{5}$ ---> $5x\sqrt{5} + 5x\sqrt{12 \cdot 5} = \sqrt{5}$

Divide all terms by $\sqrt{5}$ to simplify,

$5x\sqrt{5} + 5x\sqrt{12 \cdot 5} = \sqrt{5}$ ---> $5x + 5x\sqrt{12} = 1$

Next, factor out from the left-hand side:

$5x + 5x\sqrt{12} = 1$ ---> $5x(1+ \sqrt{12}) = 1$

Isolate by dividing by $5(1+\sqrt{12})$ and simplifying:

$5x(1+ \sqrt{12}) = 1$ ---> $x = \frac{1}{5+5\sqrt{12}}$

Last, simplify the denominator:

$x = \frac{1}{5+5\sqrt{12}}$ ----> $x = \frac{1}{5+10\sqrt{3}}$

Report an Error

Example Question #7 : How To Find The Common Factor Of Square Roots

Solve for :

$x\sqrt{23} - x\sqrt{69} = 12\sqrt{115}$

Possible Answers:

$x = \frac{1-\sqrt{5}}{12\sqrt{23}}$

$x = \frac{12\sqrt{5}}{1-\sqrt{3}}$

$x = \frac{12\sqrt{3}}{1-\sqrt{5}}$

$x = \frac{12\sqrt{23}}{1-\sqrt{3}}$

$x = \frac{1-\sqrt{3}}{12\sqrt{5}}$

Correct answer:

$x = \frac{12\sqrt{5}}{1-\sqrt{3}}$

Explanation:

Right away, we notice that $\sqrt{23}$ is a prime radical, so no simplification is possible. Note, however, that both other radicals are divisible by $\sqrt{23}$ .

Our first step then becomes simplifying the equation by dividing everything by $\sqrt{23}$ :

$x\sqrt{23} - x\sqrt{69} = 12\sqrt{115}$ ---> $x-x\sqrt{3} = 12\sqrt{5}$

Next, factor out from the left-hand side:

$x-x\sqrt{3} = 12\sqrt{5}$ ---> $x(1-\sqrt{3}) = 12\sqrt{5}$

Lastly, isolate :

$x(1-\sqrt{3}) = 12\sqrt{5}$ ---> $x = \frac{12\sqrt{5}}{1-\sqrt{3}}$

Report an Error

Example Question #1 : How To Find The Common Factor Of Square Roots

Solve for :

$-4x\sqrt{\frac{1}{4}} + \frac{2}{3}x\sqrt{27} = \sqrt{15}$

Possible Answers:

$x= \frac{\sqrt{2}}{-3+2\sqrt{15}}$

$x= \frac{\sqrt{15}}{2+2\sqrt{3}}$

$x= \frac{\sqrt{15}}{-2-3\sqrt{2}}$

$x= \frac{\sqrt{15}}{-2+2\sqrt{3}}$

$x= \frac{\sqrt{5}}{-2+2\sqrt{3}}$

Correct answer:

$x= \frac{\sqrt{15}}{-2+2\sqrt{3}}$

Explanation:

Once again, there are no common perfect squares under the radical, but with some simplification, the equation can still be solved for :

$-4x\sqrt{\frac{1}{4}} + \frac{2}{3}x\sqrt{27} = \sqrt{15}$ ---> $(\frac{1}{2}\cdot -4x) + (3 \cdot\frac{2}{3}x\sqrt{3}) = \sqrt{15}$

Simplify:

$(\frac{1}{2}\cdot -4x) + (3 \cdot\frac{2}{3}x\sqrt{3}) = \sqrt{15}$ ---> $(-2x) + (2x\sqrt{3}) = \sqrt{15}$

Factor out from the left-hand side:

$(-2x) + (2x\sqrt{3}) = \sqrt{15}$ ---> $2x(-1 + \sqrt{3}) = \sqrt{15}$

Lastly, isolate :

$2x(-1 + \sqrt{3}) = \sqrt{15}$ ---> $x= \frac{\sqrt{15}}{-2+2\sqrt{3}}$

Report an Error

← Previous 1 2 3 4 5 6 7 Next →

View ACT Math Tutors

Gary
Certified Tutor

SUNY at Albany, Bachelor of Science, Economics. Pace University-New York, Masters in Business Administration, Analysis and Fu...

View ACT Math Tutors

Stephen
Certified Tutor

Grinnell College, Bachelor in Arts, Computer Science.

View ACT Math Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

GMAT Courses & Classes in New York City, ACT Courses & Classes in Philadelphia, SSAT Courses & Classes in Atlanta, SSAT Courses & Classes in Phoenix, MCAT Courses & Classes in Houston, LSAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Boston, MCAT Courses & Classes in Los Angeles, LSAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Washington DC

Popular Test Prep

GMAT Test Prep in Chicago, SSAT Test Prep in Washington DC, ISEE Test Prep in Boston, GRE Test Prep in Chicago, GRE Test Prep in Seattle, ACT Test Prep in Philadelphia, LSAT Test Prep in Los Angeles, ISEE Test Prep in Philadelphia, SSAT Test Prep in Denver, MCAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Basic Squaring / Square Roots

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #1 : How To Find The Common Factor Of Square Roots

Example Question #2 : How To Find The Common Factor Of Square Roots

Example Question #21 : Arithmetic

Example Question #1 : How To Find The Common Factor Of Square Roots

Example Question #1 : Factoring Common Factors Of Squares And Square Roots

Example Question #4 : How To Find The Common Factor Of Square Roots

Example Question #5 : How To Find The Common Factor Of Square Roots

Example Question #1 : How To Find The Common Factor Of Square Roots

Example Question #7 : How To Find The Common Factor Of Square Roots

Example Question #1 : How To Find The Common Factor Of Square Roots

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: