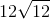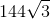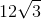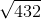Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Simplifying Square Roots

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Simplifying Square Roots

Which of the following is equal to $\sqrt{75}$ ?

Possible Answers:

$5\sqrt{3}$

$7.5\sqrt{10}$

$3\sqrt{5}$

Correct answer:

$5\sqrt{3}$

Explanation:

√75 can be broken down to √25 * √3. Which simplifies to 5√3.

Report an Error

Example Question #2 : Simplifying Square Roots

Simplify $\sqrt{a^{3}b^{4}c^{5}}$ .

Possible Answers:

$a^{2}b^{2}c^{2}\sqrt{bc}$

$ab^{2}c^{2}\sqrt{ac}$

$a^{2}b^{2}c\sqrt{ab}$

$a^{2}bc^{2}\sqrt{ac}$

$a^{2}bc\sqrt{bc}$

Correct answer:

$ab^{2}c^{2}\sqrt{ac}$

Explanation:

Rewrite what is under the radical in terms of perfect squares:

$x^{2}=x\cdot x$

$x^{4}=x^{2}\cdot x^{2}$

$x^{6}=x^{3}\cdot x^{3}$

Therefore, $\sqrt{a^{3}b^{4}c^{5}}= \sqrt{a^{2}a^{1}b^{4}c^{4}c^{1}}=ab^{2}c^{2}\sqrt{ac}$ .

Report an Error

Example Question #12 : Simplifying Square Roots

What is $\sqrt{50}$ ?

Possible Answers:

$5\sqrt{2}$

$2\sqrt{5}$

$10\sqrt{2}$

Correct answer:

$5\sqrt{2}$

Explanation:

We know that 25 is a factor of 50. The square root of 25 is 5. That leaves $\sqrt{2}$ which can not be simplified further.

Report an Error

Example Question #13 : Simplifying Square Roots

Which of the following is equivalent to $\frac{x + \sqrt{3}}{3x + \sqrt{2}}$ ?

Possible Answers:

$\frac{4x + \sqrt{5}}{3x + 2}$

$\frac{3x^{2} + 3x\sqrt{2} + x\sqrt{3} +\sqrt{6}}{9x^{2} - 2}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{9x^{2} - 2}$

$\frac{3x^{2} - \sqrt{6}}{9x^{2} + 2}$

$\frac{3x^{2} + \sqrt{6}}{3x - 2}$

Correct answer:

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{9x^{2} - 2}$

Explanation:

Multiply by the conjugate and the use the formula for the difference of two squares:

$\frac{x + \sqrt{3}}{3x + \sqrt{2}}$

$\frac{x + \sqrt{3}}{3x + \sqrt{2}}\cdot \frac{3x - \sqrt{2}}{3x - \sqrt{2}}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{(3x)^{2} - (\sqrt{2})^{2}}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{9x^{2} - 2}$

Report an Error

Example Question #5 : Properties Of Roots And Exponents

Which of the following is the most simplified form of:

$\sqrt{468}$

Possible Answers:

$4\sqrt{29}$

$\sqrt{468}$

$2\sqrt{117}$

$6\sqrt{13}$

$17\sqrt{2}$

Correct answer:

$6\sqrt{13}$

Explanation:

First find all of the prime factors of 468

$468=6\ast78=6\ast6\ast13=2\ast3\ast2\ast3\ast13$

So $\sqrt{468}=\sqrt{2\ast2\ast3\ast3\ast13}=2\ast3\sqrt{13}=6\sqrt{13}$

Report an Error

Example Question #13 : How To Simplify Square Roots

What is $\sqrt{432}$ equal to?

Possible Answers:

$6\sqrt{4}$

$12\sqrt{3}$

$144\sqrt{3}$

$6\sqrt{3}$

$12\sqrt{12}$

Correct answer:

$12\sqrt{3}$

Explanation:

$\sqrt{432}$

1. We know that 432=(144)(3) , which we can separate under the square root:

$\sqrt{144\cdot 3}$

2. 144 can be taken out since it is a perfect square: $12\cdot12=144$ . This leaves us with:

$12\sqrt{3}$

This cannot be simplified any further.

Report an Error

Example Question #5 : Simplifying Square Roots

Which of the following is equal to $\small \sqrt{420}$ ?

Possible Answers:

$\small \small 3\sqrt{70}$

$\small 4\sqrt{35}$

$\small 28\sqrt{5}$

$\small 2\sqrt{105}$

$\small 6\sqrt{35}$

Correct answer:

$\small 2\sqrt{105}$

Explanation:

When simplifying square roots, begin by prime factoring the number in question. For $\small 420$ , this is:

$\small 420 = 2*2*3*5*7$

Now, for each pair of numbers, you can remove that number from the square root. Thus, you can say:

$\small \small \sqrt{420}=2\sqrt{105}$

Another way to think of this is to rewrite $\small \small \sqrt{420}$ as $\small \sqrt{4}*\sqrt{105}$ . This can be simplified in the same manner.

Report an Error

Example Question #2 : Simplifying Square Roots

Which of the following is equivalent to $\small \sqrt{700700}$ ?

Possible Answers:

$\small 770\sqrt{13}$

$\small 90\sqrt{11}$

$\small 121\sqrt{7}$

$\small 70\sqrt{143}$

$\small 100\sqrt{77}$

Correct answer:

$\small 70\sqrt{143}$

Explanation:

When simplifying square roots, begin by prime factoring the number in question. This is a bit harder for $\small 700700$ . Start by dividing out $\small 100$ :

$\small 700700 = 7007 * 100$

Now, $\small 7007$ is divisible by , so:

$\small \small 700700 =1001 * 7 * 2*2*5*5$

$\small 1001$ is a little bit harder, but it is also divisible by $\small 7$ , so:

$\small 700700 =143*7 * 7 * 2*2*5*5$

With some careful testing, you will see that $\small 143 = 11 * 13$

Thus, we can say:

$\small \small 700700 = 2*2*5*5*7 * 7*11*13$

Now, for each pair of numbers, you can remove that number from the square root. Thus, you can say:

$\small \small \sqrt{700700} = 2*5*7*\sqrt{143}=70\sqrt{143}$

Another way to think of this is to rewrite $\small \small \small \sqrt{700700}$ as $\small \sqrt{4} * \sqrt{25} * \sqrt{49} * \sqrt{143}$ . This can be simplified in the same manner.

Report an Error

Example Question #1 : How To Simplify Square Roots

What is the simplified (reduced) form of $\sqrt{96}$ ?

Possible Answers:

$8\sqrt{3}$

$2\sqrt{24}$

$4\sqrt{6}$

It cannot be simplified further.

$2\sqrt{48}$

Correct answer:

$4\sqrt{6}$

Explanation:

To simplify a square root, you have to factor the number and look for pairs. Whenever there is a pair of factors (for example two twos), you pull one to the outside.

Thus when you factor 96 you get
$\\ \sqrt{96}=\sqrt{2\cdot 2\cdot 2\cdot2\cdot2\cdot 3}\\ \\=2\cdot 2\sqrt{2\cdot 3}\\ \\=4\sqrt{6}$

Report an Error

Example Question #3 : Simplifying Square Roots

Which of the following is equal to $\small \sqrt{1260}$ ?

Possible Answers:

$\small 26\sqrt{35}$

$\small 60\sqrt{7}$

$\small 6\sqrt{35}$

$\small 30\sqrt{3}$

$\small 10\sqrt{7}$

Correct answer:

$\small 6\sqrt{35}$

Explanation:

When simplifying square roots, begin by prime factoring the number in question. For $\small 1260$ , this is:

$\small 1260=2*2*3*3*5*7$

Now, for each pair of numbers, you can remove that number from the square root. Thus, you can say:

$\small \sqrt{1260}=2*3*\sqrt{35}=6\sqrt{35}$

Another way to think of this is to rewrite $\small \sqrt{1260}$ as $\small \sqrt{4}*\sqrt{9}*\sqrt{35}$ . This can be simplified in the same manner.

Report an Error

View ACT Math Tutors

Shane
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Computer Engineering, General.

View ACT Math Tutors

Yucheng
Certified Tutor

The University of Texas at Austin, Bachelor of Science, Mechanical Engineering.

View ACT Math Tutors

Jonathan
Certified Tutor

University of Illinois at Chicago, Bachelor in Arts, Criminal Justice. Syracuse University, Masters in Business Administratio...

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

ACT Courses & Classes in Chicago, SSAT Courses & Classes in Atlanta, GRE Courses & Classes in Chicago, ACT Courses & Classes in Miami, LSAT Courses & Classes in Phoenix, LSAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Seattle, LSAT Courses & Classes in Denver, ACT Courses & Classes in Washington DC, GMAT Courses & Classes in New York City

Popular Test Prep

ACT Test Prep in Chicago, MCAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in New York City, LSAT Test Prep in Phoenix, GRE Test Prep in Seattle, GRE Test Prep in Chicago, SSAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Denver, ACT Test Prep in Washington DC, GMAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Simplifying Square Roots

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #1 : Simplifying Square Roots

Example Question #2 : Simplifying Square Roots

Example Question #12 : Simplifying Square Roots

Example Question #13 : Simplifying Square Roots

Example Question #5 : Properties Of Roots And Exponents

Example Question #13 : How To Simplify Square Roots

Example Question #5 : Simplifying Square Roots

Example Question #2 : Simplifying Square Roots

Example Question #1 : How To Simplify Square Roots

Example Question #3 : Simplifying Square Roots

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: