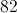Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Arithmetic

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #691 : Arithmetic

Define an operation $\blacktriangledown$ as follows:

For all real numbers a,b ,

$a \blacktriangledown b= \frac{a+1}{\left | a\right |+ \left | b\right |}$

Evaluate: $\frac{4}{5} \blacktriangledown \left (-\frac{4}{5} \right )$ .

Possible Answers:

The expression is undefined.

None of the other responses is correct.

$\frac{5}{8}$

$1 \frac{1}{8}$

Correct answer:

$1 \frac{1}{8}$

Explanation:

$a \blacktriangledown b= \frac{a+1}{\left | a\right |+ \left | b\right |}$ , or, equivalently,

$a \blacktriangledown b=\left ( a+1 \right ) \div ( | a |+ | b | )$

$\frac{4}{5} \blacktriangledown \left (-\frac{4}{5} \right )=\left ( \frac{4}{5}+1 \right ) \div \left (\left| \frac{4}{5} \right |+ \left |- \frac{4}{5}\right | \right )$

$= \frac{9}{5} \div \left ( \frac{4}{5} +\frac{4}{5} \right )$

$= \frac{9}{5} \div \frac{8}{5}$

$= \frac{9}{5} \times \frac{5}{8}$

$= \frac{9}{8}$

$=1 \frac{1}{8}$

Report an Error

Example Question #3 : Absolute Value

Define $p(x) = \frac{\left |x+2 \right |-1}{\left |x+1 \right |-2}$ .

Evaluate $p \left (-1 \frac{1}{5} \right )$ .

Possible Answers:

$-\frac{1} {9}$

$-\frac{1}{11}$

$\frac{1} {9}$

$\frac{1}{11}$

Correct answer:

$\frac{1} {9}$

Explanation:

$p(x) = \frac{\left |x+2 \right |-1}{\left |x+1 \right |-2}$ , or, equivalently,

$p(x) =\left ( \left |x+2 \right |-1 \right ) \div \left ( \left |x+1 \right |-2 \right )$

$p\left (-1 \frac{1}{5} \right )=\left ( \left |-1 \frac{1}{5}+2 \right |-1 \right ) \div \left ( \left |-1 \frac{1}{5}+1 \right |-2 \right )$

$=\left ( \left | \frac{4}{5} \right |-1 \right ) \div \left ( \left |- \frac{1}{5} \right |-2 \right )$

$=\left ( \frac{4}{5} -1 \right ) \div \left ( \frac{1}{5} -2 \right )$

$= - \frac{1}{5} \div \left ( - \frac{9}{5} \right )$

$= \frac{1}{5} \div \frac{9}{5}$

$= \frac{1}{5} \times \frac{5}{9}$

$= \frac{1} {9}$

Report an Error

Example Question #1 : How To Find Absolute Value

Define an operation $\triangleright$ as follows:

For all real numbers a,b ,

$a \triangleright b = \left | a- \frac{1}{2}b\right | + \left | \frac{1}{2} a+b\right |$

Evaluate $\frac{1}{3} \triangleright 4$ .

Possible Answers:

$6\frac{1}{2}$

$2\frac{1}{2}$

$\text{None of the other responses are correct.}$

$1\frac{1}{2}$

$5 \frac{5}{6}$

Correct answer:

$5 \frac{5}{6}$

Explanation:

$a \triangleright b = \left | a- \frac{1}{2}b\right | + \left | \frac{1}{2} a+b\right |$

$\frac{1}{3} \triangleright 4 = \left | \frac{1}{3} - \frac{1}{2} \cdot 4\right | + \left | \frac{1}{2} \cdot \frac{1}{3} +4\right |$

$= \left | \frac{1}{3} - 2\right | + \left | \frac{1}{6} +4\right |$

$= \left | -1 \frac{2}{3} \right | + \left | 4 \frac{1}{6} \right |$

$= 1 \frac{2}{3} + 4 \frac{1}{6}$

$= 5 \frac{5}{6}$

Report an Error

Example Question #692 : Arithmetic

Define $g(x)= \left | \left | 1,000- \sqrt{x}\right | - x^{3} \right |$ .

Evaluate g(16) .

Possible Answers:

$5\textup{,}092$

$3\textup{,}092$

$5\textup{,}100$

$3\textup{,}100$

$\textup{The expression is undefined.}$

Correct answer:

$3\textup{,}100$

Explanation:

$g(x)= \left | \left | 1,000- \sqrt{x}\right | - x^{3} \right |$

$g(16)= \left | \left | 1,000- \sqrt{16}\right | - 16^{3} \right |$

$= \left | \left | 1,000- 4 \right | - 16^{3} \right |$

$= \left | \left | 996 \right | - 16^{3} \right |$

$= \left | 996 - 16^{3} \right |$

$= \left | 996 - 4,096 \right |$

$= \left | -3,100 \right |$

=3,100

Report an Error

Example Question #693 : Arithmetic

Define an operation $\blacklozenge$ as follows:

For all real numbers a,b ,

$a \blacklozenge b = \left | 2a- 2b + 5 \right |$

Evaluate $(-4) \blacklozenge (-7)$

Possible Answers:

Both and

Correct answer:

Explanation:

$a \blacklozenge b = \left | 2a- 2b + 5 \right |$

$(-4) \blacklozenge (-7) = \left | 2 (-4)- 2(-7) + 5 \right |$

$= \left |-8- (-14) + 5 \right |$

$= \left |-8+14 + 5 \right |$

$= \left |11 \right |$

= 11

Report an Error

Example Question #11 : How To Find Absolute Value

What is the minimum value for if |x + 12| = 14 ?

Possible Answers:

Correct answer:

Explanation:

When solving an absolute value equation, you should remember that you can have either a positive or a negative value in the absolute value. So, for instance:

|x|=12 means that can be either or .

Thus, for this question, you know that |x + 12| = 14 can mean:

x+12 = 14

x+12 = -14

Then, you just solve each and get:

x=2

x=-26

Thus, is the minimum possible value for .

Report an Error

Example Question #694 : Arithmetic

Simplify -15*|5-22| .

Possible Answers:

405

255

Correct answer:

Explanation:

Begin by simplifying the contents of the absolute value:

-15*|5-22| = -15 * |-17|

Remember that the absolute value of a negative number is a positive value. Thus:

-15 * |-17|=-15 * 17= -255

Report an Error

Example Question #697 : Arithmetic

What is the largest possible value for if 4|3x - 5| = 64 ?

Possible Answers:

Correct answer:

Explanation:

When solving an absolute value equation, you should remember that you can have either a positive or a negative value in the absolute value. So, for instance:

|x|=12 means that can be either or .

Thus, for this question, you know that 4|3x - 5| = 64 . Start by dividing by on both sides. This will give you:

|3x - 5| = 16

Now, from this, we know:

3x - 5 = 16

3x - 5 = -16

Solve each equation for . The first is:

3x = 21

x=7

The second is 3x - 5 = -16 . You can tell that this is going to end up being negative. You do not even need to finish. The larger value will be the positive one, .

Report an Error

Example Question #13 : How To Find Absolute Value

Evaluate the following expression:

$\left | 13-24*2\right |$

Possible Answers:

-4.5

4.5

Correct answer:

Explanation:

First use order of operations (PEMDAS which stands for Parentheses, Exponents, Multiplication, Division, Addition, and Subraction) to evaluate the inner part of the absolute value:

First multiply

24*2=48 .

Then subtract that from .

13-24*2 = 13 -48 = -35 .

Absolute value means the distance away from zero, and distance is always positive.

Thus: is the answer

Report an Error

Example Question #695 : Arithmetic

Evaluate the expression if x=5 and y=7 .

$\left | 4x+3y \right | - \left | 4x-3y \right |$

Possible Answers:

Correct answer:

Explanation:

$\left | 4x+3y \right | - \left | 4x-3y \right |$

To solve, we replace each variable with the given value.

$\left | 4 (5) +3 ( 7) \right | - \left | 4 (5) -3 ( 7) \right |\ .$

$\left | 20 +21 \right | - \left | 20 -21 \right |$

Simplify. Remember that terms inside of the absolute value are always positive.

$\left | 41 \right | - \left | -1 \right |=41-1 = 40$

Report an Error

View ACT Math Tutors

Nate
Certified Tutor

University of Wisconsin-Oshkosh, non degree, Prepharmacy. University of Wisconsin-Madison, Pharmaceutical Chemist, Pharmacy.

View ACT Math Tutors

Sumit
Certified Tutor

Calcutta University, Bachelor of Science, Mathematics. Indian Statistical Institute, Master of Science, Mathematics.

View ACT Math Tutors

Jason
Certified Tutor

Brigham Young University, Bachelor, Neuroscience.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

SAT Courses & Classes in Seattle, MCAT Courses & Classes in Washington DC, MCAT Courses & Classes in Boston, ISEE Courses & Classes in Boston, ACT Courses & Classes in New York City, LSAT Courses & Classes in Atlanta, ISEE Courses & Classes in New York City, ISEE Courses & Classes in Atlanta, LSAT Courses & Classes in Boston, SSAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

ISEE Test Prep in Los Angeles, SSAT Test Prep in Washington DC, ISEE Test Prep in New York City, ISEE Test Prep in Atlanta, SSAT Test Prep in Seattle, MCAT Test Prep in Washington DC, ISEE Test Prep in Boston, ISEE Test Prep in Houston, LSAT Test Prep in Denver, ACT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Arithmetic

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #691 : Arithmetic

Example Question #3 : Absolute Value

Example Question #1 : How To Find Absolute Value

Example Question #692 : Arithmetic

Example Question #693 : Arithmetic

Example Question #11 : How To Find Absolute Value

Example Question #694 : Arithmetic

Example Question #697 : Arithmetic

Example Question #13 : How To Find Absolute Value

Example Question #695 : Arithmetic

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: