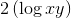Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Algebra

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #811 : Algebra

If $\frac{n^{y}}{n^{x}}=n^{6}$ for all $\dpi{100} \small n$ not equal to 0, which of the following must be true?

Possible Answers:

$\dpi{100} \small y-x = 6$

$\dpi{100} \small \frac{x}{y} = 6$

$\dpi{100} \small \frac{y}{x} = 6$

$\dpi{100} \small yx = 6$

$\dpi{100} \small y+x = 6$

Correct answer:

$\dpi{100} \small y-x = 6$

Explanation:

Remember that $\dpi{100} \small \frac{n^{y}}{n^{x}}=n^{y-x}$

Since the problem states that $\frac{n^{y}}{n^{x}}=n^{6}$ , you can assume that $\dpi{100} \small n^{y-x}=n^{6}$

This shows that $\dpi{100} \small y-x = 6$ .

Report an Error

Example Question #812 : Algebra

If and are positive integers and , then what is the value of $\frac{m}{n}$ ?

Possible Answers:

$\frac{5}{3}$

$\frac{1}{16}$

$\frac{1}{3}$

Correct answer:

Explanation:

4³= 64

Alternatively written, this is 4(4)(4) = 64 or 4³= 64^1.

Thus, m = 3 and n = 1.

m/n = 3/1 = 3.

Report an Error

Example Question #813 : Algebra

Write the following logarithm in expanded form:

$\log x^{2}y$

Possible Answers:

$\log x^{2}+\log y$

$2\log x+\log y$

$2\left ( \log xy \right )$

$2\log x-\log y$

$\log x+\log y$

Correct answer:

$2\log x+\log y$

Explanation:

$\log x^{2}y=\log x^{2}+\log y=2\log x+\log y$

Report an Error

Example Question #814 : Algebra

If and are both rational numbers and $4^{m} = 8^{n}$ , what is $\frac{m}{n}$ ?

Possible Answers:

$\frac{3}{2}$

$\frac{5}{3}$

$\frac{2}{1}$

$\frac{4}{1}$

Correct answer:

$\frac{3}{2}$

Explanation:

This question is asking you for the ratio of m to n. To figure it out, the easiest way is to figure out when 4 to an exponent equals 8 to an exponent. The easiest way to do that is to list the first few results of 4 to an exponent and 8 to an exponent and check to see if any match up, before resorting to more drastic means of finding a formula.

$4^{1} = 4, 4^{2} = 16, 4^{3} = 64, 4^{4} = 256, 4^{5} = 1024$

$8^{1}=8, 8^{2} = 64, 8^{3} = 512, 8^{4} = 4096, 8^{5} = 32768$

And, would you look at that. $4^{3}= 8^{2}$ . Therefore, $\frac{m}{n} = \frac{3}{2}$ .

Report an Error

Example Question #1 : Squaring / Square Roots / Radicals

$\small (3a-2b)^{2}$ can be rewritten as:

Possible Answers:

$\small 9a^{2}+4b^{2}$

$\small 9a^{2}+12ab+4b^{2}$

$\small 9a^{2}-4b^{2}$

$\small 9a^{2}-12ab+4b^{2}$

$\small 9a^{2}-6ab+4b^{2}$

Correct answer:

$\small 9a^{2}-12ab+4b^{2}$

Explanation:

Use the formula for solving the square of a difference, $\small (x-y)^{2}=x^{2}-2xy+y^{2}$ . In this case, $\small \small \small (3a-2b)^{2}=9a^{2}-12ab+4b^{2}$

Report an Error

Example Question #1 : Squaring / Square Roots / Radicals

Expand:

(2x-6)^2

Possible Answers:

2x^2-12x+24

4x^2-24x+36

4x-12

4x^2-12x+36

Correct answer:

4x^2-24x+36

Explanation:

To multiply a difference squared, square the first term and add two times the multiplication of the two terms. Then add the second term squared.

(2x^)^2+2(2x)(-6)+(-6)^2=4x^2-24x+36

Report an Error

Example Question #1 : How To Find The Square Of Difference

The expression $\frac{x^2-25}{x^2+11x+30}$ is equivalent to:

Possible Answers:

x+6

$\frac{x-6}{x-5}$

$\frac{x-5}{x+6}$

$\frac{x+6}{x+5}$

$\frac{x+5}{x-6}$

Correct answer:

$\frac{x-5}{x+6}$

Explanation:

First, we need to factor the numerator and denominator separately and cancel out similar terms. We will start with the numerator because it can be factored easily as the difference of two squares.

x^2 - 25 = (x + 5)(x - 5)

Now factor the quadratic in the denominator.

x^2 + 11x + 30 = (x + 5)(x + 6)

Substitute these factorizations back into the original expression.

$\frac{(x+5)(x-5)}{(x+5)(x+6)}$

The (x+5) terms cancel out, leaving us with the following answer:

$\frac{x-5}{x+6}$

Report an Error

Example Question #815 : Algebra

Evaluate the following expression:

$2^{5}+(5*2)^{2}$

Possible Answers:

110

164

132

Correct answer:

132

Explanation:

2 raised to the power of 5 is the same as multiplying 2 by itself 5 times so:

2⁵= 2x2x2x2x2 = 32

Then, 5x2 must first be multiplied before taking the exponent, yielding 10²= 100.

100 + 32 = 132

Report an Error

Example Question #2 : Squaring / Square Roots / Radicals

Expand:

(3x+5)^2

Possible Answers:

9x^2-30x+25

6x+10

9x^2+30x+25

9x^2+25

Correct answer:

9x^2+30x+25

Explanation:

To multiply a difference squared, square the first term and add two times the multiplication of the two terms. Then add the second term squared.

(3x)^2+2(3x)(5)+(5)^2=9x^2+30x+25

Report an Error

Example Question #1 : How To Find The Square Of A Sum

Which of the following is the square of 4x + 7y ?

Possible Answers:

$16x^{2}+ 22xy+ 49y^{2}$

$16x^{2}+ 28xy+ 49y^{2}$

$16x^{2}+ 56xy+ 49y^{2}$

$16x^{2} + 49y^{2}$

$16x^{2}+ 11xy+ 49y^{2}$

Correct answer:

$16x^{2}+ 56xy+ 49y^{2}$

Explanation:

Use the square of a sum pattern, substituting for and for in the pattern:

$(A+ B)^{2}= A^{2}+ 2AB + B^{2}$

$(4x + 7y)^{2}= (4x)^{2}+ 2 (4x) (7y) + (7y)^{2}$

$= 16x^{2}+ 56xy + 49y^{2}$

Report an Error

View ACT Math Tutors

Ivy
Certified Tutor

Lehigh University, Bachelor of Science, Biochemistry.

View ACT Math Tutors

Sandra
Certified Tutor

Idaho State University, Bachelor in Arts, Chemistry. Utah State University, Master of Science, Physical Chemistry.

View ACT Math Tutors

Yasmin
Certified Tutor

Johns Hopkins University, Bachelor in Arts, Mathematics.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

ISEE Courses & Classes in Los Angeles, GRE Courses & Classes in Boston, SAT Courses & Classes in Miami, LSAT Courses & Classes in Chicago, GRE Courses & Classes in Atlanta, MCAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Atlanta, SAT Courses & Classes in Atlanta, ISEE Courses & Classes in New York City, ISEE Courses & Classes in Chicago

Popular Test Prep

ACT Test Prep in San Francisco-Bay Area, SAT Test Prep in Houston, MCAT Test Prep in Boston, ISEE Test Prep in San Diego, GRE Test Prep in San Diego, ISEE Test Prep in Houston, ACT Test Prep in Washington DC, ISEE Test Prep in San Francisco-Bay Area, GMAT Test Prep in New York City, SSAT Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Algebra

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #811 : Algebra

Example Question #812 : Algebra

Example Question #813 : Algebra

Example Question #814 : Algebra

Example Question #1 : Squaring / Square Roots / Radicals

Example Question #1 : Squaring / Square Roots / Radicals

Example Question #1 : How To Find The Square Of Difference

Example Question #815 : Algebra

Example Question #2 : Squaring / Square Roots / Radicals

Example Question #1 : How To Find The Square Of A Sum

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: