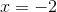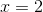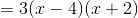64x² + 24x - 10 = 0

Factor the equation:

(8x + 5)(8x – 2) = 0

Set each side equal to zero

(8x + 5) = 0

x = -5/8

(8x – 2) = 0

x = 2/8 = 1/4

The roots of a function are the x intercepts of the function. Whenever a function passes through a point on the x-axis, the value of the function is zero. In other words, to find the roots of a function, we must set the function equal to zero and solve for the possible values of x.

This is a quadratic trinomial. Let's see if we can factor it. (We could use the quadratic formula, but it's easier to factor when we can.)

Because the coefficient in front of the is not equal to 1, we need to multiply this coefficient by the constant, which is –4. When we mutiply 2 and –4, we get –8. We must now think of two numbers that will multiply to give us –8, but will add to give us –7 (the coefficient in front of the x term). Those two numbers which multiply to give –8 and add to give –7 are –8 and 1. We will now rewrite –7x as –8x + x.

We will then group the first two terms and the last two terms.

We will next factor out a 2x from the first two terms.

Thus, when factored, the original equation becomes (2x + 1)(x – 4) = 0.

We now set each factor equal to zero and solve for x.

Subtract 1 from both sides.

2x = –1

Divide both sides by 2.

Now, we set x – 4 equal to 0.

x – 4 = 0

Add 4 to both sides.

x = 4

The roots of f(x) occur where x = .

The answer is therefore  .

36x² - 12x - 15 = 0

Factor the equation:

(6x + 3)(6x - 5) = 0

Set each side equal to zero

6x + 3 = 0

x = -3/6 = -1/2

6x – 5 = 0

x = 5/6

With quadratic equations, always begin by getting it into standard form:

Therefore, take our equation:

And rewrite it as:

You could use the quadratic formula to solve this problem.  However, it is possible to factor this if you are careful.  Factored, the equation can be rewritten as:

Now, either one of the groups on the left could be  and the whole equation would be .  Therefore, you set up each as a separate equation and solve for :

OR

The sum of these values is:

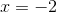
The equation can be factored.

First pull out a common factor of three from each term.

 .

Now, find the factors of the constant term that when added together result in the middle term.

The roots are what values will make the equation equal .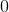  

Therefore, the answers are  and 

First you must find the solutions to the equation. This can be done either by using the quadratic formula or by simply finding two numbers whose sum is 5 and whose product is -24 and factoring the equation into (x + 8)(x – 3) = 0. The solutions to the equation are therefore -8 and 3, giving a sum of -5.

Notice that when the ball is at ground level, the height is zero. Setting s (t) equal to zero and solving for t will then give the times when the ball is at the ground.

–t² + 4t =0

t(4 – t) = 0

t = 0, t = 4

The ball returns to the ground after 4 seconds.

Define varables as  = the first number and  = the second number.  The product of the numbers is .  Solve the resulting quadratic equation by factoring and setting each factor to zero.  The numbers are 12 and 15 and the sum is 27.

We are initially presented with a quadratic equation, . To begin we must factor this equation.

The multiples of 15 are (15 and 1) and (3 and 5). The only multiples that add or subtract to  are 3 and 5. Hence we use these as our binomial numbers. . We must now decide on the signs. Because we need to add or subtract 5 and 3 to get to , both signs must be negative: .

From this point we need to switch gears to find solutions to the equation. What numbers would make this equation equal 0?

At this point split the equation into two parts.

 and  and solve.

 and . Both of these numbers inserted into the original equation will produce a result of 0.

Now the question itself is asking for the product of the solutions to the equation, or , which equals 15, therefore 15 is our answer. 

Solving for  yields  and. Solving for  yields  and .

The greatest difference between these two numbers is 14, and 14 squared is 196.