All ACT Math Resources
Example Questions
Example Question #141 : Equations / Inequalities
How many real solutions are there for the following equation?
The first thing to notice is that you have powers with a regular sequence. This means you can simply treat it like a quadratic equation. You are then able to factor it as follows:
The factoring can quickly be done by noticing that the 14 must be either 

Alternatively, one could use the quadratic formula.
The end result is that you have:
The latter of these two gives only complex answers, so there are two real answers.
Example Question #21 : How To Find The Solution To A Quadratic Equation
The formula to solve a quadratic expression is:
All of the following equations have real solutions EXCEPT:
We can use the quadratic formula to find the solutions to quadratic equations in the form ax2 + bx + c = 0. The quadratic formula is given below.
In order for the formula to give us real solutions, the value under the square root, b2 – 4ac, must be greater than or equal to zero. Otherwise, the formula will require us to find the square root of a negative number, which gives an imaginary (non-real) result.
In other words, we need to look at each equation and determine the value of b2 – 4ac. If the value of b2 – 4ac is negative, then this equation will not have real solutions.
Let's look at the equation 2x2 – 4x + 5 = 0 and determine the value of b2 – 4ac.
b2 – 4ac = (–4)2 – 4(2)(5) = 16 – 40 = –24 < 0
Because the value of b2 – 4ac is less than zero, this equation will not have real solutions. Our answer will be 2x2 – 4x + 5 = 0.
If we inspect all of the other answer choices, we will find positive values for b2 – 4ac, and thus these other equations will have real solutions.
Example Question #332 : Equations / Inequalities
Let 



We are told that f(x) = x2 - 4x + 2, and g(x) = 6 - x. Let's find expressions for f(k) and g(k).
f(k) = k2 – 4k + 2
g(k) = 6 – k
Now, we can set these expressions equal.
f(k) = g(k)
k2 – 4k +2 = 6 – k
Add k to both sides.
k2 – 3k + 2 = 6
Then subtract 6 from both sides.
k2 – 3k – 4 = 0
Factor the quadratic equation. We must think of two numbers that multiply to give us -4 and that add to give us -3. These two numbers are –4 and 1.
(k – 4)(k + 1) = 0
Now we set each factor equal to 0 and solve for k.
k – 4 = 0
k = 4
k + 1 = 0
k = –1
The two possible values of k are -1 and 4. The question asks us to find their sum, which is 3.
The answer is 3.
Example Question #581 : Algebra
What are the roots of the quadratic equation given by:
To find the roots of a quadratic equation, begin by factoring the quadratic. To do this, factor the first term (




Then, the roots are the values that make the equation zero. So set each parentheses equal to zero and solve for 
Example Question #581 : Algebra
Solve for 
Round to the nearest hundredth.
With quadratic equations, you should always start by getting all of your terms to one side of the equation, setting this equal to 
Thus, simplify 
Now, the next question you need to ask yourself is, "Can this be factored?" In this case, it can. Factor the quadratic expression:
Now, remember that you merely need to set each group equal to 


Likewise, for the other group,
Example Question #41 : How To Find The Solution To A Quadratic Equation A1
Solve for 
With quadratic equations, you should always start by getting all of your terms to one side of the equation, setting this equal to 
Thus, simplify 
Now, the next question you need to ask yourself is, "Can this be factored?" In this case, it can, though we are sometimes a bit intimidated by 
If you FOIL this out, you will see your original equation.
Now, remember that you merely need to set each group equal to 

For the other group, you get 
Example Question #42 : How To Find The Solution To A Quadratic Equation A1
Solve for 
With quadratic equations, you should always start by getting all of your terms to one side of the equation, setting this equal to 
Thus, simplify 
Now, the next question you need to ask yourself is, "Can this be factored?" In this case, it cannot be easily factored. Therefore, you should use the quadratic formula. Recall that its general form is:
For our data, 


Thus, we have:
Simplifying, this is:
Now, simplify.
Example Question #582 : Algebra
Solve for 
With quadratic equations, you should always start by getting all of your terms to one side of the equation, setting this equal to 
Thus, simplify 
Now, the next question you need to ask yourself is, "Can this be factored?" In this case, it cannot be easily factored. Therefore, you should use the quadratic formula. Recall that its general form is:
For our data, 


Thus, we have:
Simplifying, this is:
Since 
Example Question #311 : Equations / Inequalities
Solve: 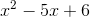
None of the other answers





To solve, we must set it equal to zero. The above expression is of the form 
to solve for the roots which are 
We can check by plugging the roots into the expression and making sure that it equals zero.
Example Question #1 : Variables
Mike wants to sell candy bars for a 

In order to solve this problem, set up the following equation:
Cross multiply:
Divide:
The original cost of the of each candy bar is
All ACT Math Resources



























































































