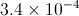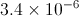In this case the exponent is positive hence you have to move the decimal point 4 places to the right from where it is in the problem giving us

In this case you have to move the decimal point 6 places to the right. When you move the decimal point to the right the exponent becomes negative.  Similarly when you move the decimal point to the left the exponent is positive.  Also, to the left of the decimal place there can be only one digit.

First, when we round to the nearest thousand we get 5, 679, 000 since we round up when the next digit is greater than 5.

Then, to put it in scientific notation, we arrange the digits so that a decimal point creates a number between 1 and 10. We get 5.679.

Then, we want the exponent of the 10 to be the number of times the decimal needs to move to the right. This is 6 times.

Thus, we get our answer.  

In order to write a number in scientific notation, you must shift the number of decimal places to get a number in the ones place.

Since the original number is a decimal, the exponent will need to be negative. This eliminates three answer choices. 

In order to get  into scientific notation with '5' in the ones place, you must shift the decimal over seven places.

Therefore, the final answer in scientific notation is .

For this, you can handle the s separately from the coefficients.  The s easily cancel:

Now, handle the coefficients like they are a separate fraction:

Notice, though, that :

Now, you need to get this into scientific notation for your answer.  It is easiest ot think of it like this:

The easiest way to work with a large number like this is to combine the  factors and then the other coefficients. After that, you will have to convert the number into scientific notation to match the answer:

Combine the powers of :

Next, combine the other coefficients:

Now, rewrite the leading number like this:

Thus, you get:

The easiest way to solve a question like this is to convert the answers all into easily comparable numbers. Remember that you move the decimal place to the left for negative powers of  and to the right for positive powers. Thus, for your number, you have:

Notice that the negative power has no influence on the sign of the number. This allows you to eliminate the negative options. The correct answer is:

When you move the decimal  places to the right, you also get:

The formula for compound interest is

where P is the principal (original) amount, r is the interest rate (in decimal form), n is the number of times per year the interest compounds, t is the time in years, and A is the final amount.

In this problem, we are solving for time, t. The given variables from the problem are:

Plugging these into the equation above, we get

This simplifies to

We can solve this by taking the natural log of both sides

The formula for compound interest is

where P is the principal (original) amount, r is the interest rate (in decimal form), n is the number of times per year the interest compounds, t is the time in years, and A is the final amount.

In this problem, we are solving for the principal, P. The given variables from the problem are:

Plugging these into the equation above, we get

Solving for P, we get

Each year, you can calculate your interest by multiplying the principle () by . For one year, this would be:

For two years, it would be:

, which is the same as 

Therefore, you can solve for a five year period by doing:

Using your calculator, you can expand the  into a series of multiplications. This gives you , which is closest to .