We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ACT Math : Algebraic Fractions

Study concepts, example questions & explanations for ACT Math

Create An Account

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #14 : Algebraic Fractions

Simplify the given fraction:

$\frac{120}{6000}$

Possible Answers:

$\frac{1}{20}$

$\frac{1}{50}$

$\frac{2}{25}$

$\frac{1}{5}$

$\frac{1}{100}$

Correct answer:

$\frac{1}{50}$

Explanation:

120 goes into 6000 evenly 50 times, so we get 1/50 as our simplified fraction.

Report an Error

Example Question #13 : Algebraic Fractions

Simplify the given fraction:

$\frac{125}{2000}$

Possible Answers:

$\frac{1}{16}$

$\frac{1}{8}$

$\frac{2}{16}$

$\frac{1}{32}$

$\frac{5}{16}$

Correct answer:

$\frac{1}{16}$

Explanation:

125 goes into 2000 evenly 16 times. 1/16 is the fraction in its simplest form.

Report an Error

Example Question #14 : Algebraic Fractions

Simplify the following expression:

$\frac{4x^6}{8x^3}$

Possible Answers:

Correct answer:

Explanation:

Following this equation, you divide 4 by 8 to get 1/2. When a variable is raised to an exponent, and you are dividing, you subtract the exponents, so 6 – 3 = 3.

Report an Error

Example Question #12 : How To Simplify A Fraction

Reduce the fraction:

$\frac{12}{96}$

Possible Answers:

$\frac{1}{8}$

$\frac{3}{24}$

$\frac{7}{12}$

$\frac{1}{4}$

$\frac{4}{16}$

Correct answer:

$\frac{1}{8}$

Explanation:

The numerator and denominator are both divisible by 12. Thus, we divide both by 12 to get our final answer.

If we instead divide by another common factor, we may need to complete the process again to make sure that we have completely reduced the fraction.

In mathematical words we get the following:

$\frac{12}{96}=\frac{1 \cdot 12}{8 \cdot 12}=\frac{1}{8}$

Report an Error

Example Question #2512 : Act Math

Simplify: $\frac{18}{54}$

Possible Answers:

$\frac{1}{3}$

$\frac{3}{9}$

$\frac{2}{9}$

$\frac{9}{27}$

$\frac{2}{3}$

Correct answer:

$\frac{1}{3}$

Explanation:

is one third of , so $\frac{18}{54}$ in its simplest form is $\frac{1}{3}$ . To reach this answer, divide both and by .

Report an Error

Example Question #11 : Algebraic Fractions

What is $\frac{6}{360}$ in its simplest form?

Possible Answers:

$\frac{6}{60}$

$\frac{1}{36}$

$\frac{1}{10}$

$\frac{1}{60}$

Correct answer:

$\frac{1}{60}$

Explanation:

To reach the answer, divide both the numerator and denominator by . After doing that, the answer is $\frac{1}{60}$ .

Report an Error

Example Question #12 : Algebraic Fractions

Simplify: $\frac{8}{64}$

Possible Answers:

$\frac{4}{8}$

$\frac{8}{64}$

$\frac{1}{8}$

$\frac{4}{64}$

$\frac{2}{8}$

Correct answer:

$\frac{1}{8}$

Explanation:

To find the answer, divide both the numerator and the denominator by . The result is $\frac{1}{8}$ .

Report an Error

Example Question #1 : How To Evaluate A Fraction

Evaluate the following equation when x=5 and round your answer to the nearest hundredth.

$\frac{x^{3}-2x^{2}-3x+5}{5x+3}$

Possible Answers:

4.33

5.00

2.32

-1.94

5.28

Correct answer:

2.32

Explanation:

$\frac{x^{3}-2x^{2}-3x+5}{5x+3}$

1. Plug in wherever there is an in the above equation.

$\frac{5^{3}-(2)(5^{2})-(3)(5)+5}{(5)(5)+3}$

2. Perform the above operations.

$\frac{5^{3}-(2)(25)-(3)(5)+5}{(5)(5)+3}$

$\frac{125-50-15+5}{25+3}$

$\frac{65}{28}=2.32$

Report an Error

Example Question #13 : Algebraic Fractions

Mary walked to school at an average speed of 2 miles per hour and jogged back along the same route at an average speed of 6 miles per hour. If her total traveling time was 1 hour, what was the total number of miles in the round trip?

Possible Answers:

Correct answer:

Explanation:

Since Mary traveled 3 times as quickly coming from school as she did going to school (6 miles per hour compared to 2 miles per hour), we know that Mary spent only a third of the time coming from school as she did going. If x represents the number of hours it took to get to school, then x/3 represents the number of hours it took her to return.

Knowing that the total trip took 1 hour, we have:

x + x/3 = 1

3x/3 + 1x/3 = 1

4x/3 = 1

x = 3/4

So we know it took Mary 3/4 of an hour to travel to school (and the remaining 1/4 of an hour to get back).

Remembering that distance = rate * time, the distance Mary traveled on her way to school was (2 miles per hour) * (3/4 of an hour) = 3/2 miles. Furthermore, since she took the same route coming back, she must have traveled 3/2 of a mile to return as well.

Therefore, the the total number of miles in Mary's round trip is 3/2 miles + 3/2 miles = 6/2 miles = 3 miles.

Report an Error

Example Question #21 : Algebraic Fractions

If $w=\frac{1}{8}$ then which of the following is equal to $w^\frac{2}{3}$ ?

Possible Answers:

$\frac{1}{4}$

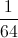
$\frac{1}{64}$

$\frac{1}{32}$

$\frac{1}{2}$

$\frac{1}{16}$

Correct answer:

$\frac{1}{4}$

Explanation:

To raise $\frac{1}{8}$ to the exponent $\frac{2}{3}$ , square $\frac{1}{8}$ and then take the cube root.

$w^\frac{2}{3}=\sqrt[3]{w^2}$

$(\frac{1}{8})^\frac{2}{3}=\sqrt[3]{(\frac{1}{8})^2}=\sqrt[3]{\frac{1}{64}}$

$\sqrt[3]{\frac{1}{64}}=\frac{1}{4}$

$(\frac{1}{8})^{\frac{2}{3}}=\frac{1}{4}$

Report an Error

View ACT Math Tutors

Dejuan
Certified Tutor

University of Illinois at Urbana-Champaign, Bachelor of Science, Electrical Engineering.

View ACT Math Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View ACT Math Tutors

Yucheng
Certified Tutor

The University of Texas at Austin, Bachelor of Science, Mechanical Engineering.

All ACT Math Resources

14 Diagnostic Tests 767 Practice Tests Question of the Day Flashcards Learn by Concept

ACT Math Tutors in Top Cities:

Atlanta ACT Math Tutors, Austin ACT Math Tutors, Boston ACT Math Tutors, Chicago ACT Math Tutors, Dallas Fort Worth ACT Math Tutors, Denver ACT Math Tutors, Houston ACT Math Tutors, Kansas City ACT Math Tutors, Los Angeles ACT Math Tutors, Miami ACT Math Tutors, New York City ACT Math Tutors, Philadelphia ACT Math Tutors, Phoenix ACT Math Tutors, San Diego ACT Math Tutors, San Francisco-Bay Area ACT Math Tutors, Seattle ACT Math Tutors, St. Louis ACT Math Tutors, Tucson ACT Math Tutors, Washington DC ACT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in Houston, ACT Courses & Classes in Boston, LSAT Courses & Classes in Philadelphia, Spanish Courses & Classes in Los Angeles, GRE Courses & Classes in Washington DC, ACT Courses & Classes in Washington DC, GRE Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Phoenix, GMAT Courses & Classes in Denver

Popular Test Prep

ACT Test Prep in Boston, LSAT Test Prep in Houston, GMAT Test Prep in Seattle, ISEE Test Prep in New York City, MCAT Test Prep in San Diego, ISEE Test Prep in Dallas Fort Worth, SSAT Test Prep in Chicago, GRE Test Prep in Miami, GRE Test Prep in Phoenix, GMAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ACT Math : Algebraic Fractions

Study concepts, example questions & explanations for ACT Math

All ACT Math Resources

Example Questions

Example Question #14 : Algebraic Fractions

Example Question #13 : Algebraic Fractions

Example Question #14 : Algebraic Fractions

Example Question #12 : How To Simplify A Fraction

Example Question #2512 : Act Math

Example Question #11 : Algebraic Fractions

Example Question #12 : Algebraic Fractions

Example Question #1 : How To Evaluate A Fraction

Example Question #13 : Algebraic Fractions

Example Question #21 : Algebraic Fractions

All ACT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: