Remember that 

Then, we can set up the equation using the given information.

Now, solve for .

Recall that the cosine of an angle is the ratio of the adjacent side to the hypotenuse of that triangle. Thus, for this triangle, we can say:

Solving for , we get:

 or 

Begin by drawing out this scenario using a little right triangle:

We know that the cosine of an angle is equal to the ratio of the side adjacent to that angle to the hypotenuse of the triangle. Thus, for our triangle, we know:

Using your calculator, solve for :

This is . Now, take the decimal portion in order to find the number of inches involved.

Thus, rounded, your answer is  feet and  inches.

Use SOH-CAH-TOA to solve for the sine of a given angle. This stands for:

.

From our triangle we see that at point , the adjacent side is side  and the hypotenuse doesn't depend upon position, it's always . Thus we get that 

In right triangles, SOHCAHTOA tells us that , and we know that  and hypotenuse . Therefore, a simple substitution and some algebra gives us our answer.

 Use a calculator or reference to approximate cosine.

 Isolate the variable term.

Thus, .

In right triangles, SOHCAHTOA tells us that , and we know that  and hypotenuse . Therefore, a simple substitution and some algebra gives us our answer.

 Use a calculator or reference to approximate cosine.

 Isolate the variable term.

Thus, .

The plane itself is effectively at the top of a right triangle, with topmost angle  and hypotenuse  feet. If this is the case, then SOHCAHTOA tells us that .

Now, solve for the adjacent:

Thus, our plane's nose is approximately  feet from the runway.

Edgar is standing on top of a right triangle because the angle from the vertical ladder to the ground is 90 degrees. To solve this question, you must know SOHCAHTOA. This acronym can be broken into three parts to solve for the sine, cosine, and tangent.

In order to solve for the missing side, you need to choose the trigonometric function that includes the side you need to find and the side that you know, relative to the angle that you know. In this case, you know the hypotenuse, so you would not use the tangent function; furthermore, you are looking for the side that is adjacent to the 68-degree angle. Thus, you need the function that incorporates adjacent and hypotenuse—the cosine function.

Typically, you would use a calculator at this point to calculate the cosine function; however, based on the answer choices provided, you can stop at this point.

In right triangles, SOHCAHTOA tells us that , and we know that  and hypotenuse . Therefore, a simple substitution and some algebra gives us our answer.

 Use a calculator or reference to approximate cosine.

 Isolate the variable term.

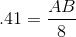
Thus, .

The domain of a function is referring to the x values that can be plugged into the function and produce a value.

The domain of the parent function  has a domain from negative infinity to positive infinity.  

The  term only shifts the function down three units, which will not affect the domain of the cosine graph.

Therefore, the answer is .