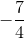Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Tangent Lines

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Coordinate Plane

There is a circle on a coordinate plain. Its perimeter passes through the point (1,0)

. At this point meets a tangent line, which also passes through the point (5,7)

. What is the slope of the line perpindicular to this tangent line?

Possible Answers:

$-\frac{4}{7}$

$\frac{7}{6}$

$\frac{4}{7}$

$-\frac{7}{4}$

$\frac{7}{4}$

Correct answer:

$-\frac{4}{7}$

Explanation:

In this kind of problem, it's important to keep track of information given about your line of interest. In this case, the coordinates given set up the stage for us to be able to get to our line of focus - the line perpendicular to the tangent line. In order to determine the perpendicular line's slope, the tangent line's slope must be calculated. Keeping in mind that:

$slope =\frac{rise}{run}=\frac{\Delta y}{\Delta x} =\frac{y_2-y_1}{x_2-x_1}$

where y2,x2 and y1,x1 are assigned arbitrarily as long as the order of assignment is maintained.

$\frac{y_2-y_1}{x_2-x_1}=\frac{7-0}{5-1}=\frac{7}{4}$ which is the slope of the tangent line.

To calculate the perpendicular line, we have to remember that the product of the tangent slope and the perpendicular slope will equal -1.

$\frac{7}{4} x \frac{?}{?} = -1$ , the perpendicular slope can then be calculated as $\frac{-4}{7}$

Report an Error

Example Question #1 : Tangent Lines

Find the slope of a tangent line at point (1,5) if the equation is -2x+3y=6 .

Possible Answers:

$\frac{2}{3}$

$\frac{1}{3}$

$-\frac{2}{3}$

Correct answer:

$\frac{2}{3}$

Explanation:

Rewrite the linear equation in standard form to slope-intercept form, y=mx+b .

-2x+3y=6

3y=2x+6

$y=\frac{2}{3}x+2$

Since the slope of every point of this line is $\frac{2}{3}$ , the slope of the tangent line at the given point should also be $\frac{2}{3}$ .

Report an Error

Example Question #1 : Tangent Lines

Find the slope of a tangent line at point (5,8) if the equation of the function is y=x^4 .

Possible Answers:

500

225

625

400

Correct answer:

500

Explanation:

To determine the slope of the function, y=x^4 , use the power rule to find the derivative function.

y=x^4

y'=4x^(^4^-^1^)=4x^3

The slope at every point of the function y=x^4 has a slope of 4x^3 . To find the slope at the given point, substitute the x-value of the given point, (5,8) , into the derivative function to find the slope.

y'=4x^3=4(5)^3=4(125)=500

Report an Error

Example Question #1 : How To Find The Equation Of A Tangent Line

Circle A is centered about the origin and has a radius of 5. What is the equation of the line that is tangent to Circle A at the point (–3,4)?

Possible Answers:

–3x + 4y = 1

3x – 4y = –1

3x – 4y = –25

3x + 4y = 7

Correct answer:

3x – 4y = –25

Explanation:

The line must be perpendicular to the radius at the point (–3,4). The slope of the radius is given by Actmath_7_113_q7

The radius has endpoints (–3,4) and the center of the circle (0,0), so its slope is –4/3.

The slope of the tangent line must be perpendicular to the slope of the radius, so the slope of the line is ¾.

The equation of the line is y – 4 = (3/4)(x – (–3))

Rearranging gives us: 3x – 4y = -25

Report an Error

Example Question #1 : How To Find The Equation Of A Tangent Line

Find the equation of a tangent line at point (2,3) if the function is y=-3x+1 .

Possible Answers:

y=-3x+6

y=-3x+3

y=-3x+9

y=-3x+2

y=-3x-3

Correct answer:

y=-3x+9

Explanation:

To find the slope of the tangent line, it is necessary to determine the slope of the function.

The function y=-3x+1 is already in the slope-intercept form, y=mx+b , and m=-3 .

Substitute the slope and the given point (2,3) into the slope-intercept equation.

3=(-3)(2)+b

3=-6+b

b=9

Substitute the known slope and the y-intercept to the slope-intercept form.

y=-3x+9

Report an Error

View SSAT- Upper Level Tutors

Gabby
Certified Tutor

University of Oregon, Bachelor in Arts, Journalism. University of Oregon, Current Grad Student, Communication, General.

View SSAT- Upper Level Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SSAT- Upper Level Tutors

Carneta
Certified Tutor

Langston University, Bachelor in Arts, Theater Arts.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Philadelphia, MCAT Tutors in Los Angeles, GMAT Tutors in Houston, Chemistry Tutors in Dallas Fort Worth, Reading Tutors in Houston, GMAT Tutors in Phoenix, Computer Science Tutors in Houston, MCAT Tutors in Dallas Fort Worth, Math Tutors in Washington DC, MCAT Tutors in Denver

Popular Courses & Classes

GRE Courses & Classes in Chicago, MCAT Courses & Classes in New York City, GMAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Chicago, Spanish Courses & Classes in Boston, LSAT Courses & Classes in Denver, LSAT Courses & Classes in Chicago, ACT Courses & Classes in Atlanta, MCAT Courses & Classes in Atlanta, MCAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

MCAT Test Prep in Boston, MCAT Test Prep in Washington DC, GMAT Test Prep in Washington DC, ISEE Test Prep in Boston, ACT Test Prep in Atlanta, SAT Test Prep in Phoenix, ACT Test Prep in Boston, LSAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Atlanta, LSAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Tangent Lines

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #1 : Coordinate Plane

Example Question #1 : Tangent Lines

Example Question #1 : Tangent Lines

Example Question #1 : How To Find The Equation Of A Tangent Line

Example Question #1 : How To Find The Equation Of A Tangent Line

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: