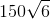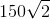We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : How to find the area of an equilateral triangle

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #4 : Equilateral Triangles

An equilateral triangle is circumscribed about a circle of radius 16. Give the area of the triangle.

Possible Answers:

The correct answer is not among the other choices.

$768 \sqrt{2}$

$3,072\sqrt{3}$

$768 \sqrt{3}$

$3,072\sqrt{2}$

Correct answer:

$768 \sqrt{3}$

Explanation:

The circle and triangle referenced are below, along with a radius to one side and a segment to one vertex:

Equilateral

$\Delta ABO$ is a 30-60-90 triangle, so

$AB = OB \cdot \sqrt{3} = 16 \sqrt{3}$

$\overline{AB}$ is one-half of a side of the triangle, so the sidelength is $32\sqrt{3}$ . The area of the triangle is

$A = \frac{s^{2} \sqrt{3}}{4} = \frac{(32\sqrt{3})^{2} \sqrt{3}}{4} = \frac{1,024 \cdot 3 \cdot \sqrt{3}}{4}= 768 \sqrt{3}$

Report an Error

Example Question #1 : How To Find The Area Of An Equilateral Triangle

Equilateral

In the above diagram, $\Delta ABC$ is equilateral. Give its area.

Possible Answers:

1,024

$512 \sqrt{3}$

The correct answer is not among the other responses.

$512 \sqrt{6}$

$512 \sqrt{2}$

Correct answer:

The correct answer is not among the other responses.

Explanation:

The interior angles of an equilateral triangle all measure 60 degrees, so, by the 30-60-90 Theorem,

$BM = \frac{AM}{\sqrt{3}} = \frac{32}{\sqrt{3}}$

Also, is the midpoint of $\overline{BC}$ , so $BC = 2 \cdot BM = \frac{64}{\sqrt{3}}$ ; this is the base.

The area of this triangle is half the product of the base and the height :

$A= \frac{1}{2} \cdot 32 \cdot \frac{64}{\sqrt{3}}= \frac{1,024}{\sqrt{3}} = \frac{1,024\cdot \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}}= \frac{1,024 \sqrt{3}}{3}$

This answer is not among the given choices.

Report an Error

Example Question #733 : Ssat Upper Level Quantitative (Math)

The perimeter of an equilateral triangle is $30\sqrt{6}$ . Give its area.

Possible Answers:

$75\sqrt{3}$

$150\sqrt{3}$

$150\sqrt{6}$

$75\sqrt{6}$

$150\sqrt{2}$

Correct answer:

$150\sqrt{3}$

Explanation:

An equilateral triangle with perimeter $30\sqrt{6}$ has three congruent sides of length

$s = 30\sqrt{6}\div 3 = 10\sqrt{6}$

The area of this triangle is

$A = \frac{s^{2}\sqrt{3}}{4} = \frac{ \left ( 10\sqrt{6} \right )^{2}\sqrt{3}}{4} = \frac{100 \cdot 6 \cdot \sqrt{3}}{4} = 150\sqrt{3}$

Report an Error

Example Question #1 : How To Find The Area Of An Equilateral Triangle

Hexagon ABCDEF is regular and has perimeter 72. $\Delta ACE$ is constructed. What is its area?

Possible Answers:

$144\sqrt{3}$

$54\sqrt{3}$

$108 \sqrt{3}$

$36\sqrt{3}$

$72 \sqrt{3}$

Correct answer:

$108 \sqrt{3}$

Explanation:

Since the perimeter of the (six-congruent-sided) regular hexagon is 72, each side has length one sixth this, or 12.

The figure described is given below, with a perpendicular segment drawn from to side $\overline{AC}$ :

Hexagon

Each angle of a regular hexagon measures $120^{\circ}$ . Therefore, $m \angle ABM = 60^{\circ }$ , and $\Delta ABM$ is a 30-60-90 triangle.

By the 30-60-90 Theorem,

$BM = \frac{1}{2}AB = \frac{1}{2} \cdot 12 = 6$

and

$AM = BM \sqrt{3} = 6 \sqrt{3}$

$AC = 2 \cdot AM = 2 \cdot 6 \sqrt{3} =12 \sqrt{3}$ .

$\Delta ACE$ is equilateral, and $12 \sqrt{3}$ is its sidelength, making its area

$A = \frac{s^{2}\sqrt{3}}{4} = \frac{\left (12 \sqrt{3} \right )^{2}\sqrt{3}}{4} = \frac{144 \cdot 3 \cdot \sqrt{3}}{4} =108 \sqrt{3}$

Report an Error

Example Question #2 : How To Find The Area Of An Equilateral Triangle

The perimeter of an equilateral triangle is . Give its area.

Possible Answers:

$81 \sqrt{3}$

$108\sqrt{2}$

$81 \sqrt{2}$

$108\sqrt{3}$

108

Correct answer:

$81 \sqrt{3}$

Explanation:

An equilateral triangle with perimeter 54 has three congruent sides of length

$s = 51 \div 3 = 18$

The area of this triangle is

$A = \frac{s^{2}\sqrt{3}}{4} = \frac{18^{2}\sqrt{3}}{4} = \frac{324 \sqrt{3}}{4}= 81 \sqrt{3}$

Report an Error

Example Question #2 : How To Find The Area Of An Equilateral Triangle

An equilateral triangle is inscribed inside a circle of radius . Give the area of the triangle.

Possible Answers:

$\frac{1,323 \sqrt{3}}{4}$

$1,323 \sqrt{3}$

$2,646\sqrt{3}$

$441\sqrt{3}$

$\frac{3,969\sqrt{3}}{4}$

Correct answer:

$1,323 \sqrt{3}$

Explanation:

The trick is to know that the circumscribed circle, or the circumcircle, has as its center the intersection of the three altitudes of the triangle, and that this center, or circumcenter, divides each altitude into two segments, one twice the length of the other - the longer one being a radius. Because of this, we can construct the following:

Equilateral

Each of the six smaller triangles is a 30-60-90 triangle, and all six are congruent.

We will find the area of $\Delta COY$ , and multiply it by 6.

By the 30-60-90 Theorem, $CY = OY \cdot \sqrt{3} = 21\sqrt{3}$ , so the area of $\Delta COY$ is

$A = \frac{1}{2}\cdot OY \cdot CY = \frac{1}{2} \cdot 21\cdot 21\sqrt{3} =\frac{ 441 \sqrt{3}}{2}$ .

Six times this - $6 \cdot \frac{ 441 \sqrt{3}}{2} = 1,323 \sqrt{3}$ - is the area of $\Delta ABC$ .

Report an Error

Example Question #3 : How To Find The Area Of An Equilateral Triangle

An equilateral triangle has side lengths of . What is the area of this triangle?

Possible Answers:

$x^2\sqrt3$

$\sqrt3$

$4\sqrt3$

$4x^2\sqrt3$

Correct answer:

$x^2\sqrt3$

Explanation:

The area of an equilateral triangle can be found using this formula:

$\frac{\sqrt3}{4}(\text{side length})^2$

Using $\text{side length}=2x$ , we can find the area of the equilateral triangle.

$\text{Area}=\frac{\sqrt3}{4}4x^2=x^2\sqrt3$

Report an Error

View SSAT- Upper Level Tutors

Grace
Certified Tutor

University of Evansville, Bachelor of Science, Archaeology.

View SSAT- Upper Level Tutors

Omar
Certified Tutor

Arizona State University, Bachelors, Civil Engineering.

View SSAT- Upper Level Tutors

Carneta
Certified Tutor

Langston University, Bachelor in Arts, Theater Arts.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Philadelphia, GMAT Tutors in Chicago, GMAT Tutors in Boston, Algebra Tutors in Boston, French Tutors in Denver, Statistics Tutors in Atlanta, French Tutors in Seattle, GRE Tutors in San Diego, English Tutors in Denver, Computer Science Tutors in Philadelphia

Popular Courses & Classes

GRE Courses & Classes in Phoenix, GMAT Courses & Classes in San Diego, GMAT Courses & Classes in New York City, LSAT Courses & Classes in Chicago, MCAT Courses & Classes in Denver, Spanish Courses & Classes in Washington DC, SAT Courses & Classes in Chicago, Spanish Courses & Classes in Seattle, SAT Courses & Classes in Boston, SAT Courses & Classes in New York City

Popular Test Prep

SSAT Test Prep in Dallas Fort Worth, SAT Test Prep in Houston, ACT Test Prep in Miami, SSAT Test Prep in Chicago, MCAT Test Prep in Dallas Fort Worth, SAT Test Prep in San Diego, SSAT Test Prep in Phoenix, SAT Test Prep in Seattle, SAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : How to find the area of an equilateral triangle

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #4 : Equilateral Triangles

Example Question #1 : How To Find The Area Of An Equilateral Triangle

Example Question #733 : Ssat Upper Level Quantitative (Math)

Example Question #1 : How To Find The Area Of An Equilateral Triangle

Example Question #2 : How To Find The Area Of An Equilateral Triangle

Example Question #2 : How To Find The Area Of An Equilateral Triangle

Example Question #3 : How To Find The Area Of An Equilateral Triangle

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: