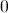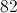Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : How to find absolute value

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #45 : Algebra

$\left | -2^{3} + 3 (4^{2})\right |$

Possible Answers:

Correct answer:

Explanation:

The first step to solving is to use the Order of Operations.

$\left |-8 + 3 (16) \right |$

$\left | -8 +48 \right |$

The absolute value $\left | x\right |$ of a real number x is the non-negative value of x without regard to its sign. The absolute value of a number is the distance of that number from the point of origin or zero on a number line.

$\left | 40\right | = 40$

Report an Error

Example Question #42 : Algebra

$3 \left | \frac{1}{2} x +2\right | > 12$

Possible Answers:

x>4 and x< -12

x>4 and x<12

x<4 and x>12

x < 4 and x> -12

Correct answer:

x>4 and x< -12

Explanation:

To solve this Absolute Value inequality, remove the Absolute Value bars and create two linear inequalities.

$3 (\frac{1}{2}x) + 6> 12$

$3 (\frac{1}{2}x) + 6 < -12$

Then, using the Order of Operations and the method for solving multi-step equations solve.

First inequality:

$3 (\frac{1}{2}x) + 6> 12$

$\frac{3}{2}x + 6 > 12$

$\frac{3}{2}x + 6 - 6 >12 -6$

$\frac{3}{2}x >6$

$\frac{3}{2}x (\frac{2}{3}) >\frac{6}{1} (\frac{2}{3})$

x> 4

Second inequality:

$\frac{3}{2}x +6 < -12$

$\frac{3}{2}x +6 -6 < -12 -6$

$\frac{3}{2}x < -18$

$\frac{3}{2}x (\frac{2}{3}) < -\frac{18}{1} (\frac{2}{3})$

x< -12

The solution to $3\left | \frac{1}{2}x +2 \right | > 12$ consists of the two intervals x > 4 and x < -12 . This pair of inequalities is the solution.

Report an Error

Example Question #43 : Algebra

$\left |4x + 4 \right | < 16$

Possible Answers:

x< -3 and x> -5

x>3 and x< -5

x < 3 and x> -5

x < 3 and x = 5

Correct answer:

x < 3 and x> -5

Explanation:

To solve this Absolute Value inequality, remove the Absolute Value bars and create two linear inequalities.

4x + 4 < 16 and

4x + 14 > -16

Then solve each of the inequalities.

First inequality:

4x + 4 < 16

4x +4 - 4 < 16-4

4x < 12

$\frac{4x}{4} < \frac{12}{4}$

x < 3

Second inequality:

4x + 14> -16

4x + 4 -4 > -16-4

4x > -20

$\frac{4x}{4}> \frac{-20}{4}$

x> -5

The solution to consists of the two intervals x< 3 and x > -5 . This pair of inequalities is the solution.

Report an Error

Example Question #21 : How To Find Absolute Value

$\left | 7x\right |\geq28$

Possible Answers:

$x\leq 4$ and $x \geq -4$

$x\geq 7$ and $x\leq -7$

$x\leq-4$ and $x\geq 4$

$x\leq 7$ and $x\geq -7$

Correct answer:

$x\leq-4$ and $x\geq 4$

Explanation:

To solve this Absolute value inequality, remove the absolute value bars and create two linear inequalities and solve.

$7x\geq 28$

$x\geq4$

$7x \leq -28$

$x \leq -4$

The solution to $\left | 7x\right | \geq 28$ consists of the two intervals $x\geq4$ and $x \leq -4$ .

This pair of inequalities is the solution.

Report an Error

Example Question #47 : Algebra

$-\left |-8- 2 (5-2)^{2} \right |$

Possible Answers:

Correct answer:

Explanation:

Step One: Order of Operations

$-\left |-8 - 2 x 3^{2} \right |$

$-\left | -8-2x9\right |$

$-\left | -8-18\right |$

$-\left | -26\right |$

The absolute value of is 26. However, because there is a negative sign outside the Absolute value bars, you would multiply the by to get the solution.

The correct answer is

Report an Error

Example Question #51 : Ssat Upper Level Quantitative (Math)

Micah is seeking new employment. The salary that he desires must be $4,000 per month with a tolerance of $600. Which absolute value inequality can be used to assess the salary which will be tolerable?

Possible Answers:

$\left | s-600\right |\geq 4,000$

$\left | s-4000\right |\geq 600$

$\left | s-4000\right | \leq 600$

$\left | s-600\ \right | \leq 4,000$

Correct answer:

$\left | s-4000\right | \leq 600$

Explanation:

$\left | s-4000\right | \leq 600$ is the correct solution.

This absolute value inequality states that the difference between the salary of $4,000 must be less than or equal to $600 to be tolerable.

Report an Error

Example Question #22 : Absolute Value

In order to ride the roller coaster at the local amusement park, children must be 145cm tall with a tolerance of 5cm. Which of the following absolute value inequalities can be used to assess which heights will be tolerable?

Possible Answers:

$\left |h-145 \right | \geq 5$

$\left | h-145\right | \leq 5$

$\left | h-5\right |\leq 145$

$\left | h-5\right | \geq 145$

Correct answer:

$\left | h-145\right | \leq 5$

Explanation:

$\left | h-145\right | \leq 5$ is the correct solution.

This Absolute Value inequality states that the difference between the children's height and 145cm must be less than or equal to 5cm .

Report an Error

Example Question #23 : Absolute Value

Using <, >, or = compare the following absolute value.

$\left | -9\right |$ __________ $\left | -7\right |$

Possible Answers:

$\left | -9\right |\leq \left | -7\right |$

$\left | -9\right |=\left | -7\right |$

$\left | -9\right |< \left | -7\right |$

$\left | -9\right |> \left | -7\right |$

Correct answer:

$\left | -9\right |> \left | -7\right |$

Explanation:

The absolute value of a number is its distance from zero. The absolute value of a negative integer is a positive integer. The distance from zero to on a number line is , so

$\left | -9\right | = 9$

The absolute value of a number is its distance from zero. The absolute value of a negative integer is a positive integer. The distance from 0 to on a number line is . Therefore:

$\left | -7\right | = 7$

Therefore

$\left | -9\right |> \left | -7\right |$

because

9>7

Report an Error

Example Question #52 : Ssat Upper Level Quantitative (Math)

Evaluate the expression if x=5 and y=7 .

$\left | 4x+3y \right | - \left | 4x-3y \right |$

Possible Answers:

Correct answer:

Explanation:

$\left | 4x+3y \right | - \left | 4x-3y \right |$

To solve, we replace each variable with the given value.

$\left | 4 (5) +3 ( 7) \right | - \left | 4 (5) -3 ( 7) \right |\ .$

$\left | 20 +21 \right | - \left | 20 -21 \right |$

Simplify. Remember that terms inside of the absolute value are always positive.

$\left | 41 \right | - \left | -1 \right |=41-1 = 40$

Report an Error

Example Question #53 : Ssat Upper Level Quantitative (Math)

Evaluate: $\begin{vmatrix}\; \; \left | 5- 3 \cdot 4\right |-8 \right \;\end{vmatrix}$

Possible Answers:

Correct answer:

Explanation:

$\begin{vmatrix}\; \; \left | 5- 3 \cdot 4\right |-8 \right \;\end{vmatrix}=\begin{vmatrix}\; \; \left | 5- 12\right |-8 \right \;\end{vmatrix}=\begin{vmatrix}\; \; \left | -7\right |-8 \right \;\end{vmatrix}=| 7 - 8| = | -1| = 1$

Report an Error

View SSAT- Upper Level Tutors

Isabela
Certified Tutor

Faculty of Law Academy of Police, Bachelor of Science, Forensic Science. Faculty of Law Academy of Police, Master of Laws, La...

View SSAT- Upper Level Tutors

Colin
Certified Tutor

Cooper Union for the Advancement of Science and Art, Bachelor of Fine Arts, Fine and Studio Arts Management. The University o...

View SSAT- Upper Level Tutors

Magda
Certified Tutor

Heritage College, Bachelor of Science, Education.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Chicago, SSAT Tutors in Philadelphia, LSAT Tutors in Seattle, French Tutors in Denver, ISEE Tutors in Atlanta, SSAT Tutors in Dallas Fort Worth, Spanish Tutors in Seattle, Physics Tutors in San Diego, Spanish Tutors in Phoenix, Biology Tutors in Miami

Popular Courses & Classes

GMAT Courses & Classes in Phoenix, GRE Courses & Classes in Seattle, ACT Courses & Classes in Washington DC, ISEE Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Atlanta, GMAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Chicago, SAT Courses & Classes in Boston, ISEE Courses & Classes in Miami, MCAT Courses & Classes in Boston

Popular Test Prep

ACT Test Prep in New York City, SAT Test Prep in San Francisco-Bay Area, GRE Test Prep in San Francisco-Bay Area, SAT Test Prep in Phoenix, MCAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Philadelphia, MCAT Test Prep in Los Angeles, GMAT Test Prep in Phoenix, SSAT Test Prep in Philadelphia, LSAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : How to find absolute value

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #45 : Algebra

Example Question #42 : Algebra

Example Question #43 : Algebra

Example Question #21 : How To Find Absolute Value

Example Question #47 : Algebra

Example Question #51 : Ssat Upper Level Quantitative (Math)

Example Question #22 : Absolute Value

Example Question #23 : Absolute Value

Example Question #52 : Ssat Upper Level Quantitative (Math)

Example Question #53 : Ssat Upper Level Quantitative (Math)

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: