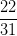Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Geometry

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #71 : Geometry

Find the equation of the line that passes through (0,5) and (1,1) .

Possible Answers:

y=-4x+1

y=-4x+5

$y=\frac{1}{4}x-1$

y=4x+1

Correct answer:

y=-4x+5

Explanation:

First, notice that our -intercept for this line is ; we can tell this because one of the points, (0,5) , is on the -axis since it has a value of for .

Now, we need to find the slope of the line. We can do that by using the slope equation:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

We can substitute in the values of the provided points— 0=x_1 , 5=y_1 , 1=x_2 and 1=y_2 —and then solve for the slope of the line that connects them:

$\text{Slope}=\frac{1-5}{1-0}=-4$

Now, put the two pieces of information together and substitute them into the y=mx+b equation to solve the problem:

y=-4x+5

Report an Error

Example Question #72 : Geometry

Find the equation of the line that passes through the points (0,3) and (-2,1) .

Possible Answers:

y=-x+3

y=x+9

y=x+3

y=x-3

Correct answer:

y=x+3

Explanation:

First, notice that our -intercept for this line is ; we can tell this because one of the points, (0,3) , is on the -axis since it has a value of for .

Now, we need to find the slope of the line. We can do that by using the slope equation:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

We can substitute in the values of the provided points— 0=x_1 , 3=y_1 , -2=x_2 and 1=y_2 —and then solve for the slope of the line that connects them:

$\text{Slope}=\frac{1-3}{-2-0}=\frac{-2}{-2}=1$

Now, put the two pieces of information together and substitute them into the y=mx+b equation to solve the problem:

y=x+3

Report an Error

Example Question #73 : Geometry

Find the equation of the line that passes through the points $(0, -1)\text{ and }(2,5)$ .

Possible Answers:

y=-3x-1

$y=\frac{1}{3}x-1$

y=3x-1

y=2x-8

Correct answer:

y=3x-1

Explanation:

First, notice that our -intercept for this line is ; we can tell this because one of the points, (0,-1) , is on the -axis since it has a value of for .

Now, we need to find the slope of the line. We can do that by using the slope equation:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

We can substitute in the values of the provided points— 0=x_1 , -1=y_1 , 2=x_2 and 5=y_2 —and then solve for the slope of the line that connects them:

$\text{Slope}=\frac{5-(-1)}{2-0}=\frac{6}{2}=3$

Now, put the two pieces of information together and substitute them into the y=mx+b equation to solve the problem:

y=3x-1

Report an Error

Example Question #74 : Geometry

Find the equation of the line that passes through the points (1, 1) and (6, 5) .

Possible Answers:

$y=\frac{4}{5}x+\frac{1}{5}$

$y=\frac{4}{5}x-1$

y=4x+1

$y=\frac{4}{5}x$

Correct answer:

$y=\frac{4}{5}x+\frac{1}{5}$

Explanation:

First, we need to find the slope of the line. We can do that by using the slope equation:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

We can substitute in the values of the provided points— 1=x_1 , 1=y_1 , 6=x_2 and 5=y_2 —and then solve for the slope of the line that connects them:

$\text{Slope}=\frac{5-1}{6-1}=\frac{4}{5}$

Next, plug one of the points' coordinates and the slope to the y=mx+b equation and solve for to find the -intercept. For this example, let's use the point (6,5) :

$5=\frac{4}{5}(6)+b$

Multiply:

$5=\frac{24}{5}+b$

Change from a whole number to a mixed number with in the denominator, just like in the fraction $\frac{24}{5}$ :

$5\cdot\frac{5}{5}=\frac{24}{5}+b$

$\frac{25}{5}=\frac{24}{5}+b$

Subtract $\frac{24}{5}$ from each side of the equation:

$b=\frac{1}{5}$

Finally, put the slope and the -intercept into the y=mx+b equation to arrive at the correct answer:

$y=\frac{4}{5}x+\frac{1}{5}$

Report an Error

Example Question #21 : Lines

Find the equation of the line that passes through (0, -2) and (4,2) .

Possible Answers:

y=x-2

y=x+2

y=-x-2

y=x-4

Correct answer:

y=x-2

Explanation:

First, notice that our -intercept for this line is ; we can tell this because one of the points, (0,-2) , is on the -axis since it has a value of for .

Now, we need to find the slope of the line. We can do that by using the slope equation:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

We can substitute in the values of the provided points— 0=x_1 , -2=y_1 , 4=x_2 and 2=y_2 —and then solve for the slope of the line that connects them:

$\text{Slope}=\frac{2-(-2)}{4-0}=\frac{4}{4}=1$

Now, put the two pieces of information together and substitute them into the y=mx+b equation to solve the problem:

y=x-2

Report an Error

Example Question #21 : Coordinate Geometry

One end of a board that is four feet long is on the ground. The other end is balanced on a box that is one foot tall, creating a slope. What is the slope of the board?

Possible Answers:

$1\frac{1}{4}$

$\frac{1}{4}$

Correct answer:

$\frac{1}{4}$

Explanation:

The slope of a line is equal to $\frac{rise}{run}$ .

Given that the box is one foot tall, the rise will be equal to "1."

Given that the board is four feet long, the run will be equal to "4."

Therefore, the slope is equal to $\frac{rise}{run}=\frac{1}{4}$ .

Report an Error

Example Question #22 : Lines

A line is given with the equation 3y-18x=21 . What is the slope of this line?

Possible Answers:

Correct answer:

Explanation:

To find the slope, put the equation in y=mx+b form.

3y-18x=21

3y=18x+21

y=6x+7

Since m=6 , that must be the slope of the line.

Report an Error

Example Question #21 : Lines

A line has the equation 8x-7y=14 . What is the slope of the line?

Possible Answers:

$-\frac{7}{8}$

$\frac{8}{7}$

$\frac{7}{8}$

$-\frac{8}{7}$

Correct answer:

$\frac{8}{7}$

Explanation:

Change the equation into the more familiar y=mx+b form. The value of will be the slope.

8x-7y=14

7y=8x-14

$y=\frac{8}{7}x-2$

Report an Error

Example Question #22 : Coordinate Geometry

What is the slope of a line that passes through the points $(15, -2)\text{ and }(-16, 20)$ ?

Possible Answers:

$-\frac{31}{22}$

$-\frac{22}{31}$

$\frac{31}{22}$

$\frac{22}{31}$

Correct answer:

$-\frac{22}{31}$

Explanation:

Use the following formula to find the slope:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

Plug in the given points to find the slope.

$Slope=\frac{20-(-2)}{-16-15}=-\frac{22}{31}$

Report an Error

Example Question #3 : How To Find Slope Of A Line

Find the slope of the line that passes through the points $(-9, 2)\text{ and }(-2, -2)$

Possible Answers:

$-\frac{7}{4}$

$\frac{4}{7}$

$\frac{7}{4}$

$-\frac{4}{7}$

Correct answer:

$-\frac{4}{7}$

Explanation:

Use the following formula to find the slope:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

$\text{Slope}=\frac{-2-2}{-2-(-9)}=-\frac{4}{7}$

Report an Error

View SSAT- Upper Level Tutors

Brooke
Certified Tutor

New York University, Bachelor in Arts, Drama and Dance Teacher Education. Georgia State University, Master of Arts, Communica...

View SSAT- Upper Level Tutors

Carneta
Certified Tutor

Langston University, Bachelor in Arts, Theater Arts.

View SSAT- Upper Level Tutors

Gabby
Certified Tutor

University of Oregon, Bachelor in Arts, Journalism. University of Oregon, Current Grad Student, Communication, General.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Washington DC, Statistics Tutors in Miami, GRE Tutors in Chicago, Spanish Tutors in Miami, French Tutors in Dallas Fort Worth, Calculus Tutors in Boston, Chemistry Tutors in Dallas Fort Worth, SSAT Tutors in Washington DC, SAT Tutors in Seattle, GRE Tutors in Seattle

Popular Courses & Classes

ISEE Courses & Classes in Phoenix, Spanish Courses & Classes in Miami, MCAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Seattle, MCAT Courses & Classes in Atlanta, ISEE Courses & Classes in Atlanta, GMAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Philadelphia, ISEE Courses & Classes in Boston, Spanish Courses & Classes in Boston

Popular Test Prep

MCAT Test Prep in Phoenix, GMAT Test Prep in San Diego, ACT Test Prep in New York City, MCAT Test Prep in San Diego, ISEE Test Prep in Denver, GMAT Test Prep in Atlanta, SAT Test Prep in Washington DC, GMAT Test Prep in Philadelphia, GMAT Test Prep in Phoenix, ISEE Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Geometry

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #71 : Geometry

Example Question #72 : Geometry

Example Question #73 : Geometry

Example Question #74 : Geometry

Example Question #21 : Lines

Example Question #21 : Coordinate Geometry

Example Question #22 : Lines

Example Question #21 : Lines

Example Question #22 : Coordinate Geometry

Example Question #3 : How To Find Slope Of A Line

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: