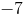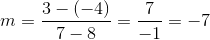Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Geometry

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #41 : Coordinate Geometry

What is the slope of the line represented by the equation $6y-16x=7$ ?

Possible Answers:

$16$

$6$

$-16$

$\frac{8}{3}$

$\frac{7}{6}$

Correct answer:

$\frac{8}{3}$

Explanation:

To rearrange the equation into a $y=mx+b$ format, you want to isolate the $y$ so that it is the sole variable, without a coefficient, on one side of the equation.

First, add $11x$ to both sides to get $6y=7+16x$ .

Then, divide both sides by 6 to get $y=\frac{7+16x}{6}$ .

If you divide each part of the numerator by 6, you get $y=\frac{7}{6}+\frac{16x}{6}$ . This is in a $y=b+mx$ form, and the $m$ is equal to $\frac{16}{6}$ , which is reduced down to $\frac{8}{3}$ for the correct answer.

Report an Error

Example Question #222 : Geometry

What is the slope of the given linear equation?

2x + 4y = -7

Possible Answers:

-2

1/2

-1/2

-7/2

Correct answer:

-1/2

Explanation:

We can convert the given equation into slope-intercept form, y=mx+b, where m is the slope. We get y = (-1/2)x + (-7/2)

Report an Error

Example Question #1 : How To Find The Slope Of A Line

What is the slope of the line:

$\frac{14}{3}x=\frac{1}{6}y-7$

Possible Answers:

$\frac{1}{28}$

$-\frac{1}{28}$

Correct answer:

Explanation:

First put the question in slope intercept form (y = mx + b):

–(1/6)y = –(14/3)x – 7 =>

y = 6(14/3)x – 7

y = 28x – 7.

The slope is 28.

Report an Error

Example Question #2 : How To Find The Slope Of A Line

What is the slope of a line that passes though the coordinates $(5,2)$ and $(3,1)$ ?

Possible Answers:

$-\frac{1}{2}$

$\frac{1}{2}$

$4$

$-\frac{2}{3}$

$\frac{2}{3}$

Correct answer:

$\frac{1}{2}$

Explanation:

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{1-2}{3-5}=\frac{-1}{-2}=\frac{1}{2}$

Report an Error

Example Question #41 : Coordinate Geometry

What is the slope of a line running through points (7,3) and (8,-4) ?

Possible Answers:

$\frac{7}{3}$

$-\frac{1}{7}$

Correct answer:

Explanation:

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{3-(-4)}{7-8}=\frac{7}{-1}=-7$

Report an Error

Example Question #42 : Coordinate Geometry

Find the slope of the line that goes through the points $(7, 15)\text{ and }(-3, -12)$

Possible Answers:

$-\frac{27}{10}$

$-\frac{10}{27}$

$\frac{27}{10}$

$\frac{10}{27}$

Correct answer:

$\frac{27}{10}$

Explanation:

Use the following formula to find the slope:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

Plug in the given points to find the slope.

$\text{Slope}=\frac{-12-15}{-3-7}=\frac{-27}{-10}=\frac{27}{10}$

Report an Error

Example Question #43 : Coordinate Geometry

Which of the following points is on both the line

y=3x-2

and the line

$\frac{1}{2}y+3x=17$

Possible Answers:

(3,16)

(4,10)

(1,1)

(6,16)

(6,-2)

Correct answer:

(4,10)

Explanation:

In the multiple choice format, you can just plug in these points to see which satisfies both equations. (1,1) and (6,16) work for the first but not the second, and (3,16) and (6,-2) work for the second but not the first. Only (4,10) works for both.

Alternatively (or if you were in a non-multiple choice scenario), you could set the equations equal to each other and solve for one of the variables. So, for instance,

y=3x-2

and y=-6x+34

so 3x-2=-6x+34

Now you can solve and get x=4 . Plug this back into either of the original equations and get y=10 .

Report an Error

Example Question #1 : How To Find Out If A Point Is On A Line With An Equation

A line has the equation y=8x-1 . Which of the following points lies on the line?

Possible Answers:

(0,8)

(3, 25)

(2, 17)

(-2, -17)

Correct answer:

(-2, -17)

Explanation:

Plug the x-coordinate of an answer choice into the equation to see if the y-coordinate matches with what comes out of the equation.

For x=-2 ,

y=8(-2)-1=-17

Report an Error

Example Question #1 : How To Find Out If A Point Is On A Line With An Equation

Which of the following points lies on the line with equation y=4x+2 ?

Possible Answers:

(-2, 12)

(1, 5)

(2, 10)

(0,4)

Correct answer:

(2, 10)

Explanation:

To find which point lies on the line, plug in the x-coordinate value of an answer choice into the equation. If the y-coordinate value that comes out of the equation matches that of the answer choice, then the point is on the line.

For x=2 ,

y=4(2)+2=10

So then, (2, 10) lies on the line.

Report an Error

Example Question #2 : How To Find Out If A Point Is On A Line With An Equation

Which of the following points lies on the line with the equation $y=\frac{1}{2}x-1$ ?

Possible Answers:

(4, 5)

(-4, -3)

(-8, 10)

(1, 0)

Correct answer:

(-4, -3)

Explanation:

To find if a point is on the line, plug in the x-coordinate of the answer choice into the given equation. If the resulting value for the y-coordinate matches that of the answer choice, then that point is on the line.

For x=-4 ,

$y=(-4)(\frac{1}{2})-1=-2-1=-3$

Report an Error

View SSAT- Upper Level Tutors

Myrtle
Certified Tutor

Southern University and A M College, Bachelor of Education, English. New Mexico State University-Main Campus, Doctor of Educ...

View SSAT- Upper Level Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SSAT- Upper Level Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Dallas Fort Worth, SSAT Tutors in San Francisco-Bay Area, Biology Tutors in Seattle, GRE Tutors in New York City, GMAT Tutors in Houston, ACT Tutors in Denver, Spanish Tutors in Miami, Algebra Tutors in Philadelphia, Biology Tutors in New York City, Biology Tutors in Boston

Popular Courses & Classes

SSAT Courses & Classes in Boston, GMAT Courses & Classes in San Diego, LSAT Courses & Classes in Washington DC, ACT Courses & Classes in Chicago, ISEE Courses & Classes in Chicago, ACT Courses & Classes in Seattle, SSAT Courses & Classes in Miami, SAT Courses & Classes in Washington DC, LSAT Courses & Classes in New York City, ACT Courses & Classes in New York City

Popular Test Prep

GMAT Test Prep in Los Angeles, GMAT Test Prep in San Francisco-Bay Area, SAT Test Prep in Phoenix, GRE Test Prep in Boston, SSAT Test Prep in Dallas Fort Worth, ACT Test Prep in Denver, MCAT Test Prep in San Diego, SSAT Test Prep in Los Angeles, ACT Test Prep in Chicago, GMAT Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Geometry

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #41 : Coordinate Geometry

Example Question #222 : Geometry

Example Question #1 : How To Find The Slope Of A Line

Example Question #2 : How To Find The Slope Of A Line

Example Question #41 : Coordinate Geometry

Example Question #42 : Coordinate Geometry

Example Question #43 : Coordinate Geometry

Example Question #1 : How To Find Out If A Point Is On A Line With An Equation

Example Question #1 : How To Find Out If A Point Is On A Line With An Equation

Example Question #2 : How To Find Out If A Point Is On A Line With An Equation

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: