All SSAT Upper Level Math Resources
Example Questions
Example Question #144 : Geometry
We have two right cylinders. The radius of the base Cylinder 1 is 
The volume of a cylinder is:
where 


So we can write:
and
Now we can summarize the given information:
Now substitute them in the 
Example Question #1922 : Hspt Mathematics
Two right cylinders have the same height. The radius of the base of the first cylinder is two times more than that of the second cylinder. Compare the volume of the two cylinders.
The volume of a cylinder is:
where 

We know that
and

So we can write:
Example Question #1 : How To Find The Volume Of A Cylinder
A cylinder has a diameter of 






Since we are given the diameter, divide that value in half to find the radius.

Now plug this value into the equation for the volume of a cylinder.


Example Question #733 : Geometry
Find the volume, in cubic inches, of a cylinder that has a radius of 






The formula to find the volume of a cylinder is 
Now, plug in the given numbers into this equation.

Example Question #734 : Geometry
Find the volume of the cylinder if the circular base has an area of 

Write the formula for volume of a cylinder.
Remember that area of a circle is
Since the area of the circle is known, substitute the area into the formula.
Example Question #1 : Areas And Perimeters Of Polygons
A regular hexagon has perimeter 9 meters. Give the length of one side in millimeters.
One meter is equal to 1,000 millimeters, so the perimeter of 9 meters can be expressed as:
9 meters = 
Since the six sides of a regular hexagon are congruent, divide by 6:

Example Question #2 : Areas And Perimeters Of Polygons
A hexagon with perimeter 60 has four congruent sides of length 

The perimeter of a polygon is the sum of the lengths of its sides. Let:

Now we can set up an equation and solve it for 

Example Question #2 : Perimeter Of Polygons
Two sides of a hexagon have a length of 


The perimeter of a polygon is the sum of the lengths of its sides. So we can write:
Example Question #3 : Areas And Perimeters Of Polygons
A regular hexagon has perimeter 15 feet. Give the length of one side in inches.
As the six sides of a regular hexagon are congruent, we can write:


One feet is equal to 12 inches, so we can write:

Example Question #1 : Perimeter Of Polygons
Each interior angle of a hexagon is 120 degrees and the perimeter of the hexagon is 120 inches. Find the length of each side of the hexagon.
Since each interior angle of a hexagon is 120 degrees, we have a regular hexagon with identical side lengths. And we know that the perimeter of a polygon is the sum of the lengths of its sides. So we can write:

Certified Tutor
All SSAT Upper Level Math Resources












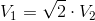
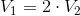
















































![Perimeter=2\left [ t+(t+1)+(t-1) \right ]=2(3t)=6t](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/111948/gif.latex)













