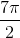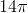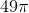Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Area and Circumference of a Circle

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #21 : Geometry

You have a circular yard and want to cover it with new sod. If you walk from the center to the fence, it is 11 feet. What would be the area of the sod?

Possible Answers:

69ft

350ft

400ft

380ft

100ft

Correct answer:

380ft

Explanation:

To find the area of a circle, the equation is $\pi r^{2}$ .

The is the radius or the distance from the center to the outside of the circle.

You would plug in the 11ft in for and that gives you an area of $\pi*11^{2}= 380ft$ .

Report an Error

Example Question #941 : Grade 7

What is the area of a circle with a diameter of , rounded to the nearest whole number?

Possible Answers:

$\dpi{100} 64$

$\dpi{100} 254$

$\dpi{100} 255$

$\dpi{100} 81$

Correct answer:

$\dpi{100} 64$

Explanation:

The formula for the area of a circle is

$\dpi{100} \pi r^{2}$

Find the radius by dividing 9 by 2:

$\dpi{100} \frac{9}{2}=4.5$

So the formula for area would now be:

$\dpi{100} \pi r^{2}=\pi (4.5)^{2}=20.25\pi \approx 63.6= 64$

Report an Error

Example Question #22 : Area And Circumference Of A Circle

Untitled

In the above diagram, the area of the shaded sector is $162 \pi$ . Evaluate .

Possible Answers:

Correct answer:

Explanation:

The area of the entire circle is equal to $\pi$ multiplied by the square of the radius, or

$\pi r ^{2} = A$

The shaded $80 ^{\circ }$ sector is equal in area to

$\frac{80}{360} = \frac{2}{9}$

that of the entire circle, so

$\frac{2}{9} A = 162 \pi$

$\frac{2}{9}\cdot \pi r ^{2} = 162 \pi$

Solving for :

$\frac{9}{2} \cdot \frac{2}{9}\cdot \pi r ^{2} = \frac{9}{2} \cdot 162 \pi$

$\pi r ^{2} = 729 \pi$

$\pi r ^{2} \div \pi = 729 \pi \div \pi$

$r ^{2} = 729$

$r = \sqrt{729} = 27$

Report an Error

Example Question #21 : Geometry

Find the area of a circle with a radius of 4.

Possible Answers:

$2\Pi$

$8\Pi$

$16\Pi$

$4\Pi$

Correct answer:

$16\Pi$

Explanation:

The formula for the area of a circle is as follows:

$A=\Pi\cdot r^{2}$

In this formula, A is area, and r is for radius. We know the radius of the circle is 4, so plug in the numbers to get the answer. Since pi is an irrational constant, it is okay to leave the answer in terms of pi.

$A=\Pi\cdot 4^{2}=16\Pi$

Report an Error

Example Question #22 : Geometry

Find the area of a circle with a radius of 12.

Possible Answers:

$96\Pi$

$144\Pi$

$12\Pi$

$24\Pi$

Correct answer:

$144\Pi$

Explanation:

The formula for the area of a circle is as follows:

$A=\Pi\cdot r^{2}$

In this formula, A is area, and r is for radius. We know the radius of the circle is 12, so plug in the numbers to get the answer. Since pi is an irrational constant, it is okay to leave the answer in terms of pi.

$A=\Pi\cdot 12^{2}=144\Pi$

Report an Error

Example Question #23 : Geometry

Find the area of a circle with a radius of 7.

Possible Answers:

$42\Pi$

$7\Pi$

$14\Pi$

$49\Pi$

Correct answer:

$49\Pi$

Explanation:

The formula for the area of a circle is as follows:

$A=\Pi\cdot r^{2}$

In this formula, A is area, and r is for radius. We know the radius of the circle is 7, so plug in the numbers to get the answer. Since pi is an irrational constant, it is okay to leave the answer in terms of pi.

$A=\Pi\cdot 7^{2}=49\Pi$

Report an Error

Example Question #24 : Geometry

Find the area of a circle with a radius of 5.

Possible Answers:

$10\Pi$

$25\Pi$

$5\Pi$

Correct answer:

$25\Pi$

Explanation:

The formula for the area of a circle is as follows:

$A=\Pi\cdot r^{2}$

In this formula, A is area, and r is for radius. We know the radius of the circle is 5, so plug in the numbers to get the answer. Since pi is an irrational constant, it is okay to leave the answer in terms of pi.

$A=\Pi\cdot 5^{2}=25\Pi$

Report an Error

Example Question #25 : Area And Circumference Of A Circle

Find the area of a circle with a diameter of 6.

Possible Answers:

$36\Pi$

$9\Pi$

$6\Pi$

$3\Pi$

Correct answer:

$9\Pi$

Explanation:

The formula for the area of a circle is as follows:

$A=\Pi\cdot r^{2}$

In this formula, A is area, and r is for radius. We know the diameter of the circle is 6, meaning we have to first find the radius. The diameter is twice the length of the radius of a circle, meaning to find radius divide the diameter by 2:

$\frac{6}{2}=3=r$

Now plug in the numbers to get the answer. Since pi is an irrational constant, it is okay to leave the answer in terms of pi.

$A=\Pi\cdot 3^{2}=9\Pi$

Report an Error

Example Question #26 : Area And Circumference Of A Circle

Find the area of a circle with a diameter of 16.

Possible Answers:

$8\Pi$

$64\Pi$

$16\Pi$

$256\Pi$

Correct answer:

$64\Pi$

Explanation:

The formula for the area of a circle is as follows:

$A=\Pi\cdot r^{2}$

In this formula, A is area, and r is for radius. We know the diameter of the circle is 16, meaning we have to first find the radius. The diameter is twice the length of the radius of a circle, meaning to find radius divide the diameter by 2:

$\frac{16}{2}=8=r$

Now plug in the numbers to get the answer. Since pi is an irrational constant, it is okay to leave the answer in terms of pi.

$A=\Pi\cdot 8^{2}=64\Pi$

Report an Error

Example Question #1 : How To Find The Circumference Of A Circle

A circle on the coordinate plane has equation

$x^{2} + y^{2} = 49$

Which of the following gives the circumference of the circle?

Possible Answers:

$\frac{49 \pi}{2}$

$14 \pi$

$49 \pi$

$\frac{7 \pi}{2}$

$7 \pi$

Correct answer:

$14 \pi$

Explanation:

The equation of a circle on the coordinate plane is

$x^{2} + y^{2} = r^{2}$

where is the radius. Therefore,

$r^{2}= 49$

and

$r = \sqrt{49} = 7$ .

The circumference of a circle is $2 \pi$ times is radius, which here would be

$C= 2 \pi \cdot 7 = 14 \pi$

Report an Error

View SSAT- Upper Level Tutors

Peter
Certified Tutor

Syracuse University, Bachelor in Arts, English. Global Learning Teaching, Certificate, Teaching English as a Second Language ...

View SSAT- Upper Level Tutors

Darron
Certified Tutor

Georgia State University, Bachelors, English Education . Liberty University, Masters, Education.

View SSAT- Upper Level Tutors

Brooke
Certified Tutor

New York University, Bachelor in Arts, Drama and Dance Teacher Education. Georgia State University, Master of Arts, Communica...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Miami, GRE Tutors in Phoenix, French Tutors in Dallas Fort Worth, Statistics Tutors in San Francisco-Bay Area, MCAT Tutors in Denver, Reading Tutors in Washington DC, Spanish Tutors in San Francisco-Bay Area, MCAT Tutors in Phoenix, Algebra Tutors in Seattle, ISEE Tutors in Phoenix

Popular Courses & Classes

LSAT Courses & Classes in Houston, ACT Courses & Classes in Houston, MCAT Courses & Classes in Atlanta, MCAT Courses & Classes in Boston, ACT Courses & Classes in Washington DC, LSAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in San Diego, LSAT Courses & Classes in Chicago, MCAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Washington DC

Popular Test Prep

LSAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Seattle, SSAT Test Prep in Boston, SAT Test Prep in Houston, SAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Boston, GRE Test Prep in San Francisco-Bay Area, ISEE Test Prep in Chicago, ACT Test Prep in Washington DC, ACT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Area and Circumference of a Circle

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #21 : Geometry

Example Question #941 : Grade 7

Example Question #22 : Area And Circumference Of A Circle

Example Question #21 : Geometry

Example Question #22 : Geometry

Example Question #23 : Geometry

Example Question #24 : Geometry

Example Question #25 : Area And Circumference Of A Circle

Example Question #26 : Area And Circumference Of A Circle

Example Question #1 : How To Find The Circumference Of A Circle

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: