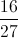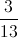We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Data Analysis / Probablility

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #5 : How To Find The Probability Of An Outcome

Three fair dice are rolled. What is the probability that none of them will show a 5 or a 6?

Possible Answers:

$\frac{4}{27}$

$\frac{16}{27}$

$\frac{4}{9}$

$\frac{8}{27}$

$\frac{2}{3}$

Correct answer:

$\frac{8}{27}$

Explanation:

The equivalent question is this: What is the probability that all three dice will show 1, 2, 3, or 4?

The probability that one fair die will show a 1, 2, 3, or 4 is $\frac{4}{6} = \frac{2}{3}$ , so the probability that all three will show 1, 2, 3, or 4 is

$\frac{2}{3} \times \frac{2}{3} \times \frac{2}{3} = \frac{8}{27}$ .

Report an Error

Example Question #6 : How To Find The Probability Of An Outcome

The threes from one standard deck of playing cards are added to another deck, and a card is drawn at random from that second, modified deck. What is the probability that that card will be an ace, a two, or a three?

Possible Answers:

$\frac{3}{14}$

$\frac{4}{13}$

$\frac{1}{4}$

$\frac{3}{13}$

$\frac{2}{7}$

Correct answer:

$\frac{2}{7}$

Explanation:

If four more threes are added to a deck of fifty-two playing cards, then the deck will have fifty-six playing cards, including four aces, four twos, and eight threes. This makes sixteen ways to draw an ace, a two, or a three out of a possible fifty-six draws, or a probability of

$\frac{16}{56} = \frac{16\div 8}{56\div 8} = \frac{2}{7}$ .

Report an Error

Example Question #5 : Outcomes

Ten balls - five green, three blue, two yellow - are placed in a hat. A ball is drawn, then replaced; then, a ball is drawn again. What is the probability that a blue ball will be drawn at least once?

Possible Answers:

$\frac{7}{15}$

$\frac{8}{15}$

$\frac{49}{100}$

$\frac{3}{10}$

$\frac{51}{100}$

Correct answer:

$\frac{51}{100}$

Explanation:

This can more easily be solved by finding the probability that neither draw will result in a blue ball, then subtracting it from 1.

The probability that the first ball will not be blue will be seven (balls that are not blue) out of ten (balls total), or $\frac{7}{10}$ . Since the ball is replaced, this is also the probability that the second will not be blue. Therefore, the probability that neither will be blue is $\frac{7}{10} \times \frac{7}{10} = \frac{49}{100}$ .

The probability that at least one draw will result in a blue ball is therefore $1- \frac{49}{100} = \frac{100}{100} - \frac{49}{100} = \frac{51}{100}$ .

Report an Error

Example Question #31 : Data Analysis / Probablility

Two fair dice are rolled. What is the probability that at least one will show a 5 or a 6?

Possible Answers:

$\frac{1}{2}$

$\frac{2}{3}$

$\frac{1}{3}$

$\frac{5}{9}$

$\frac{4}{9}$

Correct answer:

$\frac{5}{9}$

Explanation:

The best way to find this probability is to find the probability that both will show a 1, 2, 3, or 4, and subtract that probability from 1.

The probability that one fair die will show a 1, 2, 3, or 4 is $\frac{4}{6} = \frac{2}{3}$ , so the probability that both will show 1, 2, 3, or 4 is

$\frac{2}{3} \times \frac{2}{3} = \frac{4}{9}$ .

The probability that at least one die will show a 5 or a 6 is therefore

$1 - \frac{4}{9} = \frac{9}{9} - \frac{4}{9} = \frac{5}{9}$ .

Report an Error

Example Question #32 : Data Analysis / Probablility

The tens from one standard deck of playing cards are added to another deck, and a card is drawn at random from that second, modified deck. What is the probability that that card will be an ace, a two, or a three?

Possible Answers:

$\frac{4}{13}$

$\frac{2}{7}$

$\frac{3}{14}$

$\frac{3}{13}$

$\frac{1}{4}$

Correct answer:

$\frac{3}{14}$

Explanation:

If four more tens are added to a deck of fifty-two playing cards, then the deck will have fifty-six playing cards, including four aces, four twos, and four threes. This makes twelve ways to draw an ace, a two, or a three out of a possible fifty-six draws, or a probability of

$\frac{12}{56} = \frac{12\div 4}{56\div 4} = \frac{3}{14}$ .

Report an Error

Example Question #33 : Data Analysis / Probablility

A card is drawn at random from a standard 52-card deck. The person drawing wins if the card he draws is a club, a king, or a queen. What are the odds against drawing a winning card?

Possible Answers:

$35 \textrm{ to } 17$

$33 \textrm{ to } 19$

$17\textrm{ to }9$

$31 \textrm{ to } 21$

$8\textrm{ to }5$

Correct answer:

$33 \textrm{ to } 19$

Explanation:

There are 19 winning cards: the 13 clubs, the other 3 queens, and the other 3 kings (the queen and king of clubs are already counted). There are subsequently 33 losing cards, so the odds against a winning card are the number of losing cards, 33, to the number of winning cards, 19. This cannot be reduced, so the correct choice is 33 to 19.

Report an Error

Example Question #34 : Data Analysis / Probablility

A card is drawn at random from a standard 52-card deck. The person drawing wins if the card he draws is a two, a three, or a black four. What are the odds against drawing a winning card?

Possible Answers:

$21\textrm{ to }5$

$10\textrm{ to }3$

$43\textrm{ to }9$

$23\textrm{ to }3$

$11\textrm{ to }2$

Correct answer:

$21\textrm{ to }5$

Explanation:

There are 10 winning cards: the 4 twos, the 4 threes, and the 2 black fours. There are subsequently 42 losing cards, so the odds against a winning card are the number of losing cards, 42, to the number of winning cards, 10. This can be reduced to

$\frac{42}{10} = \frac{42 \div 2}{10\div 2} = \frac{21}{5}$

or 21 to 5.

Report an Error

Example Question #12 : Outcomes

A card is drawn at random from a standard 52-card deck. The person drawing wins if the card she draws is a red four or a black nine. What are the odds against drawing a winning card?

Possible Answers:

$47\textrm{ to }5$

$23\textrm{ to }3$

$45\textrm{ to }7$

$11\textrm{ to }2$

$12\textrm{ to }1$

Correct answer:

$12\textrm{ to }1$

Explanation:

There are 4 winning cards: the 2 red fours and the 2 black nines. There are subsequently 48 losing cards, so the odds against a winning card are the number of losing cards, 48, to the number of winning cards, 4. This can be reduced to

$\frac{48}{4} = \frac{48 \div 4}{4\div 4} = \frac{12}{1}$

or 12 to 1.

Report an Error

Example Question #35 : Data Analysis / Probablility

John participates in a charity fundraiser in which he pays $1 to draw a card from a standard 52-card deck. If he draws the ace of spades, he wins $25; if he draws any other ace, he wins $5; if he draws any other card, he does not win. To the nearest cent, what is the expected value of the game to John?

Possible Answers:

$-\$0.69$

$-\$0.23$

$-\$0.46$

$-\$0.77$

$\$0$

Correct answer:

$-\$0.23$

Explanation:

Since there is only one card out of 52 (ace of spades) that wins John the $25 prize, the probability of this happening is $\frac{1}{52}$ . The value of this outcome to John is $24 - the $25 prize minus the $1 he paid to play.

Since there are three cards out of 52 (ace of clubs, ace of diamonds, ace of hearts) that win John a $5 prize, the probability of this happening is $\frac{3}{52}$ . The value of this outcome to John is $4 - the $5 prize minus the $1 he paid to play.

Since there are 48 out of 52 cards that do not win John a prize, the probability of this happening is $\frac{48}{52}$ . The value of this outcome to John is $-\$1$ , since he had to pay $1 to play.

To find an expected value of a game, multiply the probability of each outcome by its value, then add the products. The expected value of this game to John is therefore

$E = \frac{1}{52} \times 24 + \frac{3}{52} \times 4 + \frac{48}{52} \times (-1)$

$E = \frac{24}{52} + \frac{12}{52} - \frac{48}{52} = - \frac{12}{52}$ dollars, or

$-12 \div 52 \approx -\$0.23$

The expected value of the game to Johnny rounds to $-\$0.23$ .

Report an Error

Example Question #11 : How To Find The Probability Of An Outcome

Sharon participates in a charity fundraiser in which she pays $2 to draw a card from a deck of cards; the deck is a standard 52-card deck plus the joker. If she draws the joker, she wins $25; if she draws the ace of spades, she wins $10; if she draws any other ace, she wins $7; if she draws any other card, she does not win. To the nearest cent, what is the expected value of the game to Sharon?

Possible Answers:

$-\$1.04$

$-\$1.00$

$-\$0.96$

$-\$0.94$

Correct answer:

$-\$0.94$

Explanation:

Since there is only one card out of 53 (joker) that wins Sharon the $25 prize, the probability of this happening is $\frac{1}{53}$ . The value of this outcome to Sharon is $23 - the $25 prize minus the $2 she paid to play.

Since there is only one card out of 53 (ace of spades) that wins Sharon the $10 prize, the probability of this happening is $\frac{1}{53}$ . The value of this outcome to Sharon is $8 - the $10 prize minus the $2 she paid to play.

Since there are three cards out of 53 (ace of clubs, ace of diamonds, ace of hearts) that win Sharon a $7 prize, the probability of this happening is $\frac{3}{53}$ . The value of this outcome to Sharon is $5 - the $7 prize minus the $2 she paid to play.

Since there are 48 out of 53 cards that do not win Sharon a prize, the probability of this happening is $\frac{48}{53}$ . The value of this outcome to Sharon is $-\$2$ , since he had to pay $2 to play.

To find an expected value of a game, multiply the probability of each outcome by its value, then add the products. The expected value of this game to Sharon is therefore

$E = \frac{1}{53} \times 23 + \frac{1}{53} \times 8 + \frac{3}{53} \times 5 + \frac{48}{53} \times (-2)$

$E = \frac{23}{53} + \frac{8}{53} + \frac{15}{53} - \frac{96}{53} = - \frac{50}{53}$ dollars, or

$-50 \div 53 \approx -\$0.94$

The expected value of the game to Sharon rounds to $-\$0.94$ .

Report an Error

View SSAT- Upper Level Tutors

Crystal
Certified Tutor

SUNY at Binghamton, Bachelor of Science, Mechanical Engineering.

View SSAT- Upper Level Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

View SSAT- Upper Level Tutors

Carneta
Certified Tutor

Langston University, Bachelor in Arts, Theater Arts.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Philadelphia, Algebra Tutors in Dallas Fort Worth, Calculus Tutors in Houston, Chemistry Tutors in Boston, MCAT Tutors in Atlanta, MCAT Tutors in Denver, Algebra Tutors in Los Angeles, Statistics Tutors in Miami, Physics Tutors in Atlanta, MCAT Tutors in Houston

Popular Courses & Classes

SAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Los Angeles, ACT Courses & Classes in Seattle, SAT Courses & Classes in Phoenix, Spanish Courses & Classes in Atlanta, MCAT Courses & Classes in New York City, MCAT Courses & Classes in Miami, Spanish Courses & Classes in Chicago, GRE Courses & Classes in New York City, LSAT Courses & Classes in Miami

Popular Test Prep

GRE Test Prep in Dallas Fort Worth, LSAT Test Prep in Philadelphia, LSAT Test Prep in Miami, SSAT Test Prep in Seattle, SAT Test Prep in Boston, LSAT Test Prep in New York City, GMAT Test Prep in Seattle, MCAT Test Prep in New York City, SAT Test Prep in San Diego, MCAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Data Analysis / Probablility

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #5 : How To Find The Probability Of An Outcome

Example Question #6 : How To Find The Probability Of An Outcome

Example Question #5 : Outcomes

Example Question #31 : Data Analysis / Probablility

Example Question #32 : Data Analysis / Probablility

Example Question #33 : Data Analysis / Probablility

Example Question #34 : Data Analysis / Probablility

Example Question #12 : Outcomes

Example Question #35 : Data Analysis / Probablility

Example Question #11 : How To Find The Probability Of An Outcome

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: