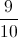SSAT Upper Level Math : Data Analysis / Probablility
Study concepts, example questions & explanations for SSAT Upper Level Math
All SSAT Upper Level Math Resources
Example Questions
Example Question #2 : How To Read Tables
The above is an annual income tax table for married couples for a given state.
Mr. Clarke earned a monthly salary of 
The correct answer is not among the other choices.
Mr. and Mrs. Clarke earned a total of
(noting that Mrs. Clarke worked for nine months)
This places them in the highest tax bracket, so they will pay $810 plus 2.3% of their income over $80,000:
Round this to $2,756.
Example Question #21 : Data Analysis / Probablility
The above is an annual income tax table for single persons in a given state.
Michael earned 
From salary, interest, and dividends, Michael earned
putting him in the 1.3% tax bracket.
His income tax will be
making $500 the correct response.
Example Question #23 : Interpretation Of Tables And Graphs
What is the probability of rolling a single die and it landing on 2 and 4?
When you roll on die you can only get one possible value facing up. The expression "the probability of getting a 2 and 4" means that they both occur at the same time. Since you can not get two results with one die, the probability must be 
Example Question #23 : Interpretation Of Tables And Graphs
What is the probability of rolling a single die and it landing on 2 and 4?
When you roll on die you can only get one possible value facing up. The expression "the probability of getting a 2 and 4" means that they both occur at the same time. Since you can not get two results with one die, the probability must be
Example Question #3 : How To Read Tables
| Column1 | Column2 |
| 1 | 0 |
| 2 | 0 |
| 3 | 2 |
| 4 | 3 |
| 5 | 4 |
| 6 | 5 |
| 7 | 8 |
| 8 | 8 |
| 9 | 8 |
| 10 | 8 |
| 11 | 5 |
| 12 | 0 |
Looking the the table given above, what is the range of the data set?
The range of the data is the difference between the highest and lowest independent variable values.
In this set, the lowest is 
The difference between these two is 
Example Question #25 : Interpretation Of Tables And Graphs
A popular word game uses one hundred tiles, each of which is marked with a letter or a blank. The distribution of the tiles is shown above, with each letter paired with the number of tiles marked with that letter. Notice that there are two blank tiles.
In the game, the four letters that are the most difficult to play are the "J", the "Q", the "X", and the "Z". John and Jane, who are in third grade, agree to remove these letters. After this is done, what percent of the letter tiles are marked with consonants (Note: "Y" counts as a consonant)?
The easiest way to count the consonants is to count the vowels and blanks first.
There are nine "A" tiles, twelve "E" tiles, nine "I" tiles, eight "O" tiles, four "U" tiles, and two "blanks". This is a total of
There are 96 tiles left after the removal of the "J", the "Q", the "X", and the "Z". Therefore, the number of consonants remaining is
This rounds to 54%.
Example Question #1 : How To Find The Probability Of An Outcome
A fair coin is tossed nine times. Each toss comes up heads. What is the probability that the coin will come up heads a tenth time?
Each flip of the coin is an independent event, and does not affect the other flips; all that matters is that the coin is fair. Because of that fact, the probability that the tenth flip comes up heads is 
Example Question #2 : How To Find The Probability Of An Outcome
Ten balls - five green, three blue, two yellow - are placed in a hat. Two balls are drawn, one after the other, without replacement. What is the probability that at least one will be green?
This can more easily be solved by finding the probability that neither will be green, then subtracting it from 1.
The probability that the first ball will be not be green is five out of ten, or 
This will leave nine balls, four not green, making the probability that the second ball will then not be green 
Multiply these probabilities:
This is the probability that neither ball is green; subtract this from 1:
Example Question #3 : Probability
Six boxes are marked with numbers 1 to 6. Each box contains ten marbles, with the number of red marbles in each box corresponding to its number, and the remainder being white.
A fair die is rolled. The box corresponding to the roll is chosen and a marble is drawn at random from that box. What is the probability of drawing a red marble?
The die is fair, making each box equally likely to be chosen; also, each marble is equally likely to be chosen after the box is chosen. This makes each marble overall equally likely to be chosen. Since there are
red marbles out of
marbles total, the probability of choosing a red marble is
Example Question #3 : Probability
Six boxes are marked with numbers 1 to 6. Each box contains ten marbles, with the number of red marbles in each box corresponding to its number, and the remainder being white.
A fair die is rolled. The box corresponding to the roll is chosen and a marble is drawn at random from that box. What is the probability of drawing a white marble?
The die is fair, making each box equally likely to be chosen; also, each marble is equally likely to be chosen after the box is chosen. This makes each marble overall equally likely to be chosen. Since there are
white marbles out of
marbles total, the probability of choosing a white marble is
Certified Tutor
Certified Tutor
All SSAT Upper Level Math Resources
