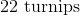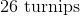All SSAT Middle Level Math Resources
Example Questions
Example Question #43 : Ratios & Proportional Relationships
Traffic from the suburbs and farms into a city typically follows an observable pattern. On any given morning there are 


In order to solve this problem we must make a table of ratios. In the question we are given the base ratio:
We can use this ratio to make a table.

According to the table, there are 
Example Question #44 : Ratios & Proportional Relationships
Traffic from the suburbs and farms into a city typically follows an observable pattern. On any given morning there are 


In order to solve this problem we must make a table of ratios. In the question we are given the base ratio:
We can use this ratio to make a table.

According to the table, there are 
Example Question #45 : Ratios & Proportional Relationships
Traffic from the suburbs and farms into a city typically follows an observable pattern. On any given morning there are 


In order to solve this problem we must make a table of ratios. In the question we are given the base ratio:
We can use this ratio to make a table.

According to the table, there are 
Example Question #41 : Ratios & Proportional Relationships
Traffic from the suburbs and farms into a city typically follows an observable pattern. On any given morning there are 


In order to solve this problem we must make a table of ratios. In the question we are given the base ratio:
We can use this ratio to make a table.

According to the table, there are 
Example Question #61 : Numbers And Operations
Traffic from the suburbs and farms into a city typically follows an observable pattern. On any given morning there are 


In order to solve this problem we must make a table of ratios. In the question we are given the base ratio:
We can use this ratio to make a table.

According to the table, there are 
Example Question #61 : Ratio And Proportion
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #61 : Numbers And Operations
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #62 : Numbers And Operations
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #51 : Ratios & Proportional Relationships
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #51 : Ratios & Proportional Relationships
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Certified Tutor
Certified Tutor
All SSAT Middle Level Math Resources