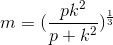We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : SAT Mathematics

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1881 : Sat Mathematics

Solve

$\frac{4x-4}{x+4}=10$

Possible Answers:

$x=\frac{22}{3}$

x=-3

$x=-\frac{22}{3}$

x=-22

Correct answer:

$x=-\frac{22}{3}$

Explanation:

$\frac{4x-4}{x+4}=10$

First multiply by the denominator on each side

$\frac{4x-4}{x+4}\cdot(x+4)=10(x+4)$

4x-4=10(x+4)

Expand left side, and solve for

4x-4=10x+40

-44=6x

$x=\frac{-44}{6}=-\frac{22}{3}$

Report an Error

Example Question #1 : How To Find The Solution To A Rational Equation With Lcd

Rational_5

Possible Answers:

–2

–1

Correct answer:

Explanation:

Rational_2

Rational_3

Rational_4

Report an Error

Example Question #2 : How To Find The Solution To A Rational Equation With Lcd

Linesmb1

Possible Answers:

–bm/(m²+ 1)

bm/(m²+ 1)

b/(m²+ 1)

–b/(m²– 1)

–b/(m + 1)

Correct answer:

b/(m²+ 1)

Explanation:

Linesmb5

Linesmb4

Report an Error

Example Question #3 : How To Find The Solution To A Rational Equation With Lcd

In the equation below, , , and are non-zero numbers. What is the value of in terms of and ?

$\frac{1}{m^3}-\frac{1}{k^2}=\frac{1}{p}$

Possible Answers:

$m=(\frac{p+k^2}{2})^3$

$m=\frac{p^2k^3}{p+k^2}$

$m=p^{\frac{1}{2}}-k^{\frac{1}{3}}$

$m=(\frac{pk^2}{p+k^2})^{\frac{1}{3}}$

$m=(\frac{p+k^2}{pk^2})^{\frac{1}{3}}$

Correct answer:

$m=(\frac{pk^2}{p+k^2})^{\frac{1}{3}}$

Explanation:

Pkm_7-21-13

Pkm2_7-21-13

Report an Error

Example Question #1 : How To Find The Solution To A Rational Equation With Lcd

Solve for x:

$\frac{x+3}{7}=3$

Possible Answers:

x=42

x=24

x=18

x=0

x=6

Correct answer:

x=18

Explanation:

The first step is to cancel out the denominator by multiplying both sides by 7:

$7\cdot \frac{x+3}{7}=3\cdot7$

x+3=21

Subtract 3 from both sides to get by itself:

x+3-3=21-3

x=18

Report an Error

Example Question #3 : How To Find The Solution To A Rational Equation With Lcd

Solve for and using elimination:

2x+3y=5

-x-2y=-8

Possible Answers:

x=-14 and y=11

x=14 and y=-11

x=8 and y=4

x=-8 and y=-4

$x=\frac{5}{2}$ and $y=\frac{5}{3}$

Correct answer:

x=-14 and y=11

Explanation:

When using elimination, you need two factors to cancel out when the two equations are added together. We can get the in the first equation to cancel out with the in the second equation by multiplying everything in the second equation by :

2x+3y=5

2(-x-2y)=2(-8)

Now our two equations look like this:

2x+3y=5

-2x-4y=-16

The can cancel with the -2x , giving us:

3y=5

-4y=-16

These equations, when summed, give us:

-y=-11

y=11

Once we know the value for , we can just plug it into one of our original equations to solve for the value of :

2x+3y=5

2x+3(11)=5

2x+33=5

2x=-28

x=-14

Report an Error

Example Question #111 : Equations / Inequalities

Give the solution set of the rational equation $\frac{(x- 5)^{2}}{(x- 4) ^{2}} = 1$

Possible Answers:

$\left \{ - \frac{1}{2}, \frac{9}{2} \right \}$

$\left \{ 5\right \}$

$\left \{ - \frac{9}{2}, \frac{9}{2} \right \}$

$\left \{ \frac{9}{2} \right \}$

$\left \{ 4, 5\right \}$

Correct answer:

$\left \{ \frac{9}{2} \right \}$

Explanation:

Multiply both sides of the equation by the denominator $(x- 4) ^{2}$ :

$\frac{(x- 5)^{2}}{(x- 4) ^{2}} \cdot (x- 4) ^{2} =1 \cdot (x- 4) ^{2}$

$(x- 5)^{2} = (x- 4) ^{2}$

Rewrite both expression using the binomial square pattern:

$x^{2} - 2 \cdot x \cdot 5+ 5^{2} = x^{2} - 2 \cdot x \cdot 4+ 4^{2}$

$x^{2} -10x + 25 = x^{2} - 8x+16$

This can be rewritten as a linear equation by subtracting $x^{2}$ from both sides:

$x^{2} -10x + 25- x^{2} = x^{2} - 8x+16 - x^{2}$

-10x + 25 = - 8x+16

Solve as a linear equation:

-10x + 25+ 8x - 25 = - 8x+16 + 8x - 25

-2x = -9

$\frac{-2x}{-2 } =\frac{ -9 }{-2}$

$x= \frac{9}{2}$

Report an Error

Example Question #2 : How To Find The Solution To A Rational Equation With Lcd

Solve:

$\frac{10-x}{40}=-5$

Possible Answers:

x=21

x=200

x=210

x=-200

x=-210

Correct answer:

x=210

Explanation:

$\frac{10-x}{40}=-5$

Multiply by on each side

10-x=-200

Subtract on each side

-x=-210

Multiply by on each side

x=210

Report an Error

Example Question #1 : Linear / Rational / Variable Equations

Find the solution to the following equation if x = 3:

y = (4x² - 2)/(9 - x²)

Possible Answers:

no possible solution

Correct answer:

no possible solution

Explanation:

Substituting 3 in for x, you will get 0 in the denominator of the fraction. It is not possible to have 0 be the denominator for a fraction so there is no possible solution to this equation.

Report an Error

Example Question #3 : Linear / Rational / Variable Equations

Undefined_denom3

I. x = 0

II. x = –1

III. x = 1

Possible Answers:

I only

II only

III only

II and III only

I, II, and III

Correct answer:

I only

Explanation:

Undefined_denom2

Report an Error

View SAT Mathematics Tutors

Kenneth
Certified Tutor

North Georgia University, Bachelors, Accounting. Brenau University, Masters, Business.

View SAT Mathematics Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Mathematics Tutors

Danielle
Certified Tutor

Penn State University, Bachelor of Science, Civil Engineering.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

ACT Courses & Classes in Boston, Spanish Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Phoenix, SAT Courses & Classes in Chicago, GRE Courses & Classes in New York City, SSAT Courses & Classes in Seattle, ACT Courses & Classes in Washington DC, ISEE Courses & Classes in Los Angeles, GMAT Courses & Classes in Miami

Popular Test Prep

GMAT Test Prep in New York City, SSAT Test Prep in Los Angeles, ACT Test Prep in Boston, SSAT Test Prep in Washington DC, MCAT Test Prep in Chicago, ACT Test Prep in Washington DC, ACT Test Prep in Atlanta, ACT Test Prep in San Francisco-Bay Area, GRE Test Prep in Denver, ISEE Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : SAT Mathematics

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #1881 : Sat Mathematics

Example Question #1 : How To Find The Solution To A Rational Equation With Lcd

Example Question #2 : How To Find The Solution To A Rational Equation With Lcd

Example Question #3 : How To Find The Solution To A Rational Equation With Lcd

Example Question #1 : How To Find The Solution To A Rational Equation With Lcd

Example Question #3 : How To Find The Solution To A Rational Equation With Lcd

Example Question #111 : Equations / Inequalities

Example Question #2 : How To Find The Solution To A Rational Equation With Lcd

Example Question #1 : Linear / Rational / Variable Equations

Example Question #3 : Linear / Rational / Variable Equations

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: