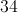We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : SAT Mathematics

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #41 : How To Find The Solution To An Equation

How much water should be added to $2\ L$ of 90% cleaning solution to yield 50% cleaning solution?

Possible Answers:

$1.2\ L$

$2.4\ L$

$0.8\ L$

$1.6\ L$

$1.5\ L$

Correct answer:

$1.6\ L$

Explanation:

Pure water is 0% and pure solution 100%. Let $x$ = water to be added.

$V_{1}P_{1} + V_{2}P_{2} = V_{f}P_{f}$ in general where $V$ is the volume and $P$ is the percent.

So the equation to solve becomes $x(0)+2(0.90)= (x+2)(0.50)$

and $x=1.6\ L$

Report an Error

Example Question #31 : Linear / Rational / Variable Equations

Solve $x+2y=14$ and $2x+y=13$

Possible Answers:

$(4,5)$

$(1,3)$

$(-4,-5)$

$(5,4)$

$(3,2)$

Correct answer:

$(4,5)$

Explanation:

This problem is a good example of the substitution method of solving a system of equations. We start by rewritting the first equation in terms of $x$ to get $x=14-2y$ and then substutite the $x$ into the second equation to get

$2(14-2y)+y=13$ .

Solving this equation gives $y=5$ and substituting this value into one of the original equations gives $x=4$ , thus the correct answer is $(4,5)$ .

Report an Error

Example Question #43 : Linear / Rational / Variable Equations

Joy bought some art supplies. She bought colored pencils for $1.25 per box and sketch pads for $2.25 each. Joy bought one more sketch pad than colored pencil boxes and spent $9.25. How many sketch pads did she buy?

Possible Answers:

$2$

$4$

$3$

$5$

$1$

Correct answer:

$3$

Explanation:

Let $x$ = # of color pencil boxes and $x+1$ = # of sketch pads purchased.

So the equation to solve becomes $1.25x+2.25(x+1)=9.25$ .

Solving this equations leads to 2 colored pencil boxes and 3 sketch pads.

Report an Error

Example Question #213 : Algebra

$\left | 2x - 3 \right |-x= 5$

Possible Answers:

$x=-8$

$x=-8\ or \ x=-\frac{3}{2}$

$x=8$

$x=-\frac{2}{3}$

$x=8\ or\ x=-\frac{2}{3}$

Correct answer:

$x=8\ or\ x=-\frac{2}{3}$

Explanation:

This question deals with absolute value equations which will normally gives you two solutions.

You need to solve two sets of equations for absolute value problems:

$2x-3 = x+5$

and

$2x-3=-\left ( x+5 \right )$

Report an Error

Example Question #71 : How To Find The Solution To An Equation

Steve sells cars. His monthly salary is $1,000. He gets a $500 commission for each car he sells. If Steve wants to make $7,500 this month, how many cars would he have to sell?

Possible Answers:

Correct answer:

Explanation:

Let = money earned and = number of cars sold

So y = 500x + 1000

7500 = 500x + 1000 and solving shows that he needs to sell 13 cars to make $7,500.

Report an Error

Example Question #1812 : Sat Mathematics

A chemistry student needs to dilute some acid. How much pure water should be added to 2 gallons of 80% acid solution to yield 20% acid solution?

Possible Answers:

$5\ gallons$

$8\ gallons$

$6\ gallons$

$4\ gallons$

$2\ gallons$

Correct answer:

$6\ gallons$

Explanation:

Let pure water = 0 % and pure acid = 100%

The general equation to use is:

$V_{1}P_{1} + V_{2}P_{2} = V_{f}P_{f}$ where is the volume and is the percent solution.

So the equation to solve becomes x(0) + 2(.80) = (x + 2)(.20) and x = 6 gallons of pure water needs to be added to get a 20% acid solution.

Report an Error

Example Question #41 : How To Find The Solution To An Equation

The Widget Company makes widgets. The monthly fixed costs are $750. It costs $45 to make each widget. The widgets sell for $75 a piece.

What is the monthly break-even point?

Possible Answers:

Correct answer:

Explanation:

The break-even point is where the costs equal revenue.

Let = # of widgets sold.

Costs: C(w) = 45w + 750

Revenue: R(w) = 75w

So the equation to solve becomes 45w + 750 = 75w

So the break-even point occurs when they sell 25 widgets.

Report an Error

Example Question #41 : Equations / Inequalities

The Widget Company makes widgets. The monthly fixed costs are $750. It costs $45 to make each widget. The widgets sells for $75 a piece.

The Widget Company wants to make a profit of $3,000. How many widgets must be sold?

Possible Answers:

125

140

150

100

Correct answer:

125

Explanation:

Profits = Revenues - Costs

Revenue: R(w) = 75w

Costs: C(w) = 45w + 750

Profit: P(w) = 75w - (45w + 750) = 30w -750

So the equation to solve becomes 3,000 = 30w - 750

So a $3,000 profit occurs when they sell 125 widgets

Report an Error

Example Question #41 : How To Find The Solution To An Equation

Sally sells custom picture frames. Her monthly fixed costs are $350. It costs $10 to make each frame. Sally sells her picture frames for $35 each.

To make a profit of $500, how many frames need to be sold?

Possible Answers:

Correct answer:

Explanation:

Let = # of frames sold

Profits = Revenues-Costs

Revenues: R(x) = 35x

Costs: C(x) = 10x + 350

Profits = P(x) = R(x) - C(x) = 35x - (10x + 350) = 25x - 350

So the equation to solve becomes 500 = 25x - 350

So 34 picture frames must be sold to make a $500 profit.

Report an Error

Example Question #222 : Algebra

How much pure water must be added to 2 gallons of 90% pure cleaning solution to yield a 30% pure cleaning solution?

Possible Answers:

$2\ gallons$

$6\ gallons$

$4\ gallons$

$2.5\ gallons$

$3\ gallons$

Correct answer:

$4\ gallons$

Explanation:

Let pure water be 0% and pure solution be 100%.

So the general equation to solve is:

$V_{1}P_{1} + V_{2}P_{2} = V_{f}P_{f}$ where is the volume and the is percent solution.

So the equation to solve becomes x(0) + 2(0.90) = (x + 2)(0.30)

Solving shows that we need to add 4 gallons of pure water to 2 gallons of 90% pure cleaning solution to get a 30% pure solution.

Report an Error

View SAT Mathematics Tutors

Kenneth
Certified Tutor

North Georgia University, Bachelors, Accounting. Brenau University, Masters, Business.

View SAT Mathematics Tutors

Arlin
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Neuroscience.

View SAT Mathematics Tutors

Thomas
Certified Tutor

Michigan State University, Bachelor in Arts, History. Central Michigan University, Doctor of Philosophy, History.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

GRE Courses & Classes in Philadelphia, SSAT Courses & Classes in Houston, Spanish Courses & Classes in Boston, SAT Courses & Classes in Phoenix, GMAT Courses & Classes in Seattle, GMAT Courses & Classes in Houston, SSAT Courses & Classes in Washington DC, Spanish Courses & Classes in Atlanta, ACT Courses & Classes in Miami, ISEE Courses & Classes in Seattle

Popular Test Prep

ISEE Test Prep in Washington DC, GMAT Test Prep in Seattle, ACT Test Prep in Washington DC, GRE Test Prep in Philadelphia, ISEE Test Prep in Chicago, LSAT Test Prep in San Diego, SSAT Test Prep in San Diego, LSAT Test Prep in New York City, SAT Test Prep in Denver, LSAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : SAT Mathematics

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #41 : How To Find The Solution To An Equation

Example Question #31 : Linear / Rational / Variable Equations

Example Question #43 : Linear / Rational / Variable Equations

Example Question #213 : Algebra

Example Question #71 : How To Find The Solution To An Equation

Example Question #1812 : Sat Mathematics

Example Question #41 : How To Find The Solution To An Equation

Example Question #41 : Equations / Inequalities

Example Question #41 : How To Find The Solution To An Equation

Example Question #222 : Algebra

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: