Every triangle has 180 degrees.  An isosceles triangle has one vertex angle and two congruent base angles. 

Solve the equation \(\displaystyle 27+27+x=180\) for x to find the measure of the vertex angle. 

x = 180 - 27 - 27

x = 126

Therefore the measure of the vertex angle is \(\displaystyle 126^{\circ}\).

Area of a triangle is ½ x base x height. Since base:height = 3:2, base = 1.5 height.  Area = 12 = ½ x 1.5 height x height or 24/1.5 = height².  Height = 4.  Base = 1.5 height = 6. Half the base and the height form the legs of a right triangle, with an equal leg of the isosceles triangle as the hypotenuse. This is a 3-4-5 right triangle.

This question is about the Triangle Inequality, which states that in a triangle with two sides A and B, the third side must be greater than the absolute value of the difference between A and B and smaller than the sum of A and B.

Applying the Triangle Inequality to this problem, we see that the third side must be greater than the absolute value of the difference between the other two sides, which is |6-6|=0, and smaller than the sum of the two other sides, which is 6+6=12. The only answer choice that does not satisfy this range of possible values is 12 since the third side must be LESS than 12.

The triangle has two sides of equal length, 13, so it is by definition isosceles. 

To determine whether the triangle is acute, right, or obtuse, compare the sum of the squares of the lengths of the two shortest sides to the square of the length of the longest side. The former quantity is equal to

\(\displaystyle 13^{2} + 13^{2} = 169 + 169 = 338\)

The latter quantity is equal to

\(\displaystyle 18^{2} = 324\)

The former is greater than the latter; consequently, the triangle is acute. The correct response is that the triangle is acute and isosceles.

In general, the formula for the area of a trapezoid is (1/2)(a + b)(h), where a and b are the lengths of the bases, and h is the length of the height. Thus, we can write the area for the trapezoid given in the problem as follows:

area of trapezoid = (1/2)(4 + s)(s)

Similarly, the area of a square with sides of length a is given by a². Thus, the area of the square given in the problem is s².

We now can set the area of the trapezoid equal to the area of the square and solve for s.

(1/2)(4 + s)(s) = s²

Multiply both sides by 2 to eliminate the 1/2.

(4 + s)(s) = 2s²

Distribute the s on the left.

4s + s² = 2s²

Subtract s² from both sides.

4s = s²

Because s must be a positive number, we can divide both sides by s.

4 = s

This means the value of s must be 4.

The answer is 4.

To solve, simply use the formula for the area of a trapezoid. Thus,

\(\displaystyle A=\frac{1}{2}(b1+b2)h=\frac{1}{2}(1+2)(2)=3\)

Let \(\displaystyle t\) be the common sidelength of the square. The area of the square is \(\displaystyle X = t^{2}\).

Construct segment \(\displaystyle \overline{MN}\). This divides the square into Rectangle \(\displaystyle AMND\) and a right triangle. The dimensions of Rectangle \(\displaystyle AMND\) are 

\(\displaystyle AD = t\)

and

\(\displaystyle ND = \frac{1}{2} CD = \frac{1}{2} t\).

The area of Rectangle \(\displaystyle AMND\) s the product of these dimensions:

\(\displaystyle A_{1} = AD \cdot ND = t \cdot \frac{1}{2} t = \frac{1}{2} t ^{2}\)

The lengths of the legs of Right \(\displaystyle \bigtriangleup MNO\) are

\(\displaystyle MN = AD = t\)

and 

\(\displaystyle NO = \frac{1}{2} CN = \frac{1}{2} \cdot \frac{1}{2} CD = \frac{1}{2} \cdot \frac{1}{2} t = \frac{1}{4} t\)

The area of this right triangle is half the product of these lengths, or

\(\displaystyle A_{2} = \frac{1}{2} \cdot MN \cdot NO = \frac{1}{2} \cdot t \cdot \frac{1}{4} t = \frac{1}{8} t ^{2}\)

This is seen below:

The sum of these areas is the area of Quadrilateral \(\displaystyle AMOD\)

\(\displaystyle A = A_{1}+ A_{2}= t^{2}+\frac{1}{8}t ^{2} = \frac{5}{8} t ^{2}\).

Substituting \(\displaystyle X\) for \(\displaystyle t^{2}\), the area is \(\displaystyle \frac{5}{8} X\).

Construct \(\displaystyle \overline{MN}\) as shown in the diagram below:

Quadrilateral \(\displaystyle AMND\) is a rectangle, so opposite sides are congruent. Therefore, \(\displaystyle MN = AD = t\).

Since \(\displaystyle N\) is the midpoint of \(\displaystyle \overline{CD}\),

\(\displaystyle CN = \frac{1}{2} CD = \frac{1}{2} t\)

Since \(\displaystyle O\) is the midpoint of \(\displaystyle \overline{CN}\), 

\(\displaystyle ON = \frac{1}{2} CN = \frac{1}{2} \cdot \frac{1}{2} t = \frac{1}{4} t\).

\(\displaystyle \bigtriangleup MNO\) is a right triangle, so, by the Pythagorean Theorem, 

\(\displaystyle MO = \sqrt{(MN)^{2}+(NO)^{2} }\)

Substituting: 

\(\displaystyle MO= \sqrt{t^{2}+\left (\frac{1}{4}t \right)^{2} }\)

\(\displaystyle MO= \sqrt{t^{2}+ \frac {1}{16} t ^{2} }\)

\(\displaystyle MO= \sqrt{ \frac {17}{16} t ^{2} }\)

Apply the Product of Radicals and Quotient of Radicals Rules:

\(\displaystyle MO= \sqrt{ \frac {17}{16} t ^{2} }\)

\(\displaystyle = \sqrt{ \frac {17}{16} } \cdot \sqrt{t^{2}}\)

\(\displaystyle = \sqrt{ \frac {17}{16} } t\)

\(\displaystyle = \frac { \sqrt{17}}{ \sqrt{16}} \cdot t\)

\(\displaystyle = \frac { \sqrt{17}}{4} t\)

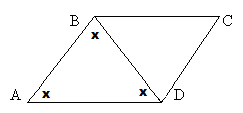
If all of the angles in triangle ABD are equal and line BD divides the parallelogram, then all angles in triangle BDC must be equal as well.

We now have two equilateral triangles, so all sides of the triangles will be equal.

All sides therefore equal 5.

5+5+5+5 = 20

To solve, simply use the formula for the area of a parallelogram. Thus,

\(\displaystyle A=lh=5*6=30\)

Don't let a parallelogram fool you. It is just like a rectangle but on a slant. As long as you are given the height, and not the slant side length, you can use the same formula.