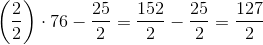First reduce the fraction. We can divide both the numerator and the denominator by 3.

Now our expression looks like this:

When you add or subtract fractions, you need to have the same denominator. The lowest common deonminator here is 2. So we need to multiply and solve:

To add , first simply each term by rewriting the terms using a division sign.

Take the reciprocal of the terms after the division sign, and change the division sign to a multiplication sign. Simplify.

The terms shown are complex fractions.  We first need to simplify each and find the least common denominator before solving.

Rewrite the complex fraction using a division sign.

Change the division sign to a multiplication sign, and take the reciprocal of the second term.

Repeat this step for the second term.

Add the two terms together.  

The answer is:  

Let x be the number of 10-person tables, and y be the number of 20-person tables. Since there are 40 tables in the cafeteria, x + y = 40. 10x represents the number of people sitting at 10-person tables, and 20y represents the number of people sitting at 20-person tables. Since the cafeteria can seat 600 people, 10x + 20y = 600. Now we have 2 equations and 2 unknowns, and can solve the system. To do this, multiply the first equation by 10 and subtract it from the second equation. This yields 0x + 10y = 200; solving for y tells us there are 20 tables that seat 20 people. Since x + y = 40, x = 20, so there are 20 tables that seat 10 people. The ratio of x:y is therefore 1:1.

The first term is m, so the second term is m/10+5 or (m+50)/10. When we take the ratio of the second term to the first term, we get (((m+50)/10))/m, which is ((m+50)/10)(1/m), or (m+50)/10m.

We first divide 630 miles by 90 miles per hour to get the amount of time it took car B to reach the destination, giving us 7 hours. We then multiply 7 hours by car A’s average speed and we get 490 miles.

Since G is the total number of male athletes that use steroids and H is the total number of female athletes that use steroids, the sum of the two is equal to I, which is the total number of all students using steroids.

The first bounce reaches a height of 175. The second bounce will equal 175 multiplied by 2/5 or 70. Repeat this process. You will get the data below. 4.48 is rounded to 4.5.

The flow of water through one pipe is 20 m³ / minute.

Thus, the flow of water through 4 pipes is 80 m³ / minute.

Since each tank is a cube with a side length of 20m, the volume of each tank is:

Volume of one tank = (20 m)³ = 8000 m³.

The total volume of two tanks is 2 * 8000 m³ = 16,000 m³

Therefore, the total minutes for 4 pipes to fill 2 tanks is:

80 m³/min

Total area of hall = 60ft * 50ft = 3000 ft²

At 1 person per 5 square feet, 3000 ft² / 5 ft² per person  = 600 people