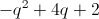Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Polynomial Operations

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Divide Polynomials

Simplify: $\frac{6x^7y^3z^9}{3x^6y^3z}$

Possible Answers:

xz^8

2xz^8

xyz^8

xyz

6xyz^8

Correct answer:

2xz^8

Explanation:

Cancel by subtracting the exponents of like terms:

$\frac{6x^7y^3z^9}{3x^6y^3z} = 2x^{7-6}y^{3-3}z^{9-1}=2xy^0z^8=2xz^8$

Report an Error

Example Question #12 : Polynomials

Divide $x^{3} + 125y ^{3}$ by x+ 5y .

Possible Answers:

$x ^{2}+ 5xy + 25y^{2}$

$x ^{2}+10xy + 25y^{2}$

$x ^{2} + 25y^{2}$

$x ^{2}-10xy + 25y^{2}$

$x ^{2}-5xy + 25y^{2}$

Correct answer:

$x ^{2}+ 5xy + 25y^{2}$

Explanation:

It is not necessary to work a long division if you recognize $x^{3} + 125y ^{3}$ as the sum of two perfect cube expressions:

$x^{3} + 125y ^{3} = x^{3} + 5^{3} y ^{3} = x^{3} + (5y )^{3}$

A sum of cubes can be factored according to the pattern

$A^{3}+ B^{3} = (A+B) (A^{2}+ AB +B^{2})$ ,

so, setting A = x, B = 5y ,

$x^{3} + (5y )^{3} =(x+5y) [x ^{2}+ x \cdot 5y + (5y)^{2}]$

$=(x+5y)(x ^{2}+ 5xy + 25y^{2})$

Therefore,

$\frac{x^{3} + 125y ^{3}}{x+ 5y} = \frac{(x+5y)(x ^{2}+ 5xy + 25y^{2})}{x+ 5y} = x ^{2}+ 5xy + 25y^{2}$

Report an Error

Example Question #374 : Algebra

By what expression can 3x+7 be multiplied to yield the product $6x^{3} +20x^{2} +5x-21$ ?

Possible Answers:

$2x^{2 }+ x - 3$

$2x^{2 } - 3$

$2x^{2 }-x - 3$

$2x^{2 }+ 2x - 3$

Correct answer:

$2x^{2 }+ 2x - 3$

Explanation:

Divide $6x^{3} +20x^{2} +5x-21$ by 3x+7 by setting up a long division.

Divide the lead term of the dividend, $6x^{3}$ , by that of the divisor, ; the result is $\frac{6x^{3}}{3x} = 2 x^{2}$

Enter that as the first term of the quotient. Multiply this by the divisor:

$2 x^{2} (3x+7) = 2 x^{2} (3x)+2 x^{2} ( 7) = 2x^{3} + 14x^{2}$

Subtract this from the dividend. This is shown in the figure below.

Division poly

Repeat the process with the new difference:

$\frac{6x^{2}}{3x} = 2 x$

$2 x (3x+7) = 2 x (3x)+2 x ( 7) = 2x^{2} + 14x$

Division poly

Repeating:

$\frac{-9x}{3x} = -3$

-3 (3x+7) = -3 (3x)+ (-3) ( 7) = -9x+ 21

Division poly

The quotient - and the correct response - is $2x^{2 }+ 2x - 3$ .

Report an Error

Example Question #2 : Polynomials

$F(x) = x^{3} + x^{2} - x + 2$

and

$G(x) = x^{2} + 5$

What is FG(x) ?

Possible Answers:

$(FG)(x) = x^{3} - x - 3$

$(FG)(x) = x^{5} + x^{4} - x^{3} + 2x^{2} - 5x -10$

$(FG)(x) = x^{5} + x^{4} - x - 2$

$(FG)(x) = x^{3} + 2x^{2} - x + 7$

$(FG)(x) = x^{5} + x^{4} +4x^{3} + 7x^{2} - 5x +10$

Correct answer:

$(FG)(x) = x^{5} + x^{4} +4x^{3} + 7x^{2} - 5x +10$

Explanation:

$(FG)(x) = F(x)G(x)$ so we multiply the two function to get the answer. We use $x^{m}x^{n} = x^{m+n}$

Report an Error

Example Question #2151 : Sat Mathematics

Find the product:

( x^4-5x+7)(x^4+2x+1)

Possible Answers:

x^4+8x^2+10x-9

x^8+7x^4-10x^2

x^6+5x^5+3x^4+x^2

x^7+9x^4-10x^2+8

x^8-3x^5+8x^4-10x^2+9x+7

Correct answer:

x^8-3x^5+8x^4-10x^2+9x+7

Explanation:

Find the product:

( x^4-5x+7)(x^4+2x+1)

Step 1: Use the distributive property.

x^4(x^4+2x+1)-5x(x^4+2x+1)+7(x^4+2x+1)

x^8+2x^5+x^4-5x^5-10x^2-5x+7x^4+14x+7

Step 2: Combine like terms.

x^8+2x^5-5x^5+x^4+7x^4-10x^2-5x+14x+7

x^8-3x^5+8x^4-10x^2+9x+7

Report an Error

Example Question #12 : Polynomials

represents a positive quantity; represents a negative quantity.

$x^{4} = 116$

$y^{2} = 11$

Evaluate $(x- y)(x+y)(x^{2} + y^{2})$

Possible Answers:

The correct answer is not among the other choices.

237

Correct answer:

Explanation:

The first two binomials are the difference and the sum of the same two expressions, which, when multiplied, yield the difference of their squares:

$(x- y)(x+y)(x^{2} + y^{2})$

$=(x^{2}- y^{2}) (x^{2} + y^{2})$

Again, a sum is multiplied by a difference to yield a difference of squares, which by the Power of a Power Property, is equal to:

$(x^{2}) ^{2} - (y^{2}) ^{2}$

$= x^{2\cdot 2} - y^{2\cdot 2}$

$= x^{4} - y^{4}$

$y^{2} = 11$ , so by the Power of a Power Property,

$(y^{2} )^{2}= 11^{2}$

$y^{2\cdot 2} = 121$

$y^{4} = 121$

Also, $x^{4} = 116$ , so we can now substitute accordingly:

$(x- y)(x+y)(x^{2} + y^{2})$

$= x^{4} - y^{4}$

= 116 - 121

= -5

Note that the signs of and are actually irrelevant to the problem.

Report an Error

Example Question #14 : Polynomials

represents a positive quantity; represents a negative quantity.

$x^{6} = 625$

$y ^{6} = 64$

Evaluate $(x-y) (x^{2}+xy+y^{2})$ .

Possible Answers:

Correct answer:

Explanation:

$(x-y) (x^{2}+xy+y^{2})$ can be recognized as the pattern conforming to that of the difference of two perfect cubes:

$(x-y) (x^{2}+xy+y^{2}) = x^{3} - y^{3}$

Additionally, by way of the Power of a Power Property,

$(x^{3})^{ 2 } = x^{3 \cdot 2} = x^{6 }$ , making $x^{3}$ a square root of $x^{6}$ , or 625; since is positive, so is $x^{3}$ , so

$x^{3} = \sqrt{625} = 25$ .

Similarly, $y ^{3}$ is a square root of $y ^{6}$ , or 64; since is negative, so is $y^{3}$ (as an odd power of a negative number is negative), so

$y^{3} = - \sqrt{64} = -8$ .

Therefore, substituting:

$(x-y) (x^{2}+xy+y^{2}) = x^{3} - y^{3} = 25 - (-8) = 25+8= 33$ .

Report an Error

Example Question #2 : How To Multiply Polynomials

and represent positive quantities.

$x^{2} = 20$

$y^{2} = 5$

Evaluate $(x-y) (x^{2}+xy+y^{2})$ .

Possible Answers:

$5 \sqrt{5}$

$45 \sqrt{15 }$

$35 \sqrt{15 }$

$35 \sqrt{5}$

$45\sqrt{5}$

Correct answer:

$35 \sqrt{5}$

Explanation:

$(x-y) (x^{2}+xy+y^{2})$ can be recognized as the pattern conforming to that of the difference of two perfect cubes:

$(x-y) (x^{2}+xy+y^{2}) = x^{3} - y^{3}$

Additionally,

$x^{2} = 20$ and is positive, so

$x = \sqrt{20}$

Using the product of radicals property, we see that

$x = \sqrt{4 \cdot 5} = \sqrt{4 } \cdot \sqrt{ 5} = 2 \sqrt{ 5}$

and

$x ^{3 } = x^{2} \cdot x = 20 \cdot 2 \sqrt{5} = 40 \sqrt{5}$

$y^{2} = 5$ and is positive, so

$y = \sqrt{5}$ ,

and

$y^{3}= y^{2} \cdot y = 5 \sqrt{5}$

Substituting for $x ^{3 }$ and $y^{3}$ , then collecting the like radicals,

$(x-y) (x^{2}+xy+y^{2})$

$= x^{3} - y^{3}$

$= 40 \sqrt{5}-5 \sqrt{5}$

$=( 40 -5 )\sqrt{5}$

$=35 \sqrt{5}$ .

Report an Error

Example Question #61 : Expressions

Simplify the following expression:

$(2q^{2}+4q+7)-(3q^{2}-5)$

Possible Answers:

$-3q^{2}+12$

$-q^{2}+4q+12$

$-5q^{2}+4q+2$

-q^2+4q+2

Correct answer:

$-q^{2}+4q+12$

Explanation:

This is not a FOIL problem, as we are adding rather than multiplying the terms in parentheses.

Add like terms together:

$2q^{2}-3q^{2}=-1q^{2}=-q^2$

has no like terms.

7-(-5)=12

Combine these terms into one expression to find the answer:

$-q^{2}+4q+12$

Report an Error

View SAT Mathematics Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

View SAT Mathematics Tutors

Sharif
Certified Tutor

NCCU, Bachelors, Physics and Mathematics.

View SAT Mathematics Tutors

Miriam
Certified Tutor

Washington University in St Louis, Bachelor in Arts, Biology, General.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

Spanish Courses & Classes in Phoenix, GMAT Courses & Classes in Philadelphia, SAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Los Angeles, ISEE Courses & Classes in Seattle, LSAT Courses & Classes in Philadelphia, SSAT Courses & Classes in Miami, SAT Courses & Classes in Miami, LSAT Courses & Classes in Seattle

Popular Test Prep

ISEE Test Prep in Miami, MCAT Test Prep in Seattle, ACT Test Prep in Seattle, SSAT Test Prep in New York City, GMAT Test Prep in Philadelphia, MCAT Test Prep in Miami, SSAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Dallas Fort Worth, GRE Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Polynomial Operations

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #2 : How To Divide Polynomials

Example Question #12 : Polynomials

Example Question #374 : Algebra

Example Question #2 : Polynomials

Example Question #2151 : Sat Mathematics

Example Question #12 : Polynomials

Example Question #14 : Polynomials

Example Question #2 : How To Multiply Polynomials

Example Question #61 : Expressions

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: