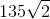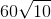Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : How to find the perimeter of a hexagon

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Hexagons

Hexagon

Archimedes High School has an unusual track in that it is shaped like a regular hexagon, as above. Each side of the hexagon measures 264 feet.

Alvin runs at a steady speed of seven miles an hour for twelve minutes, starting at point A and working his way clockwise. When he is finished, which of the following points is he closest to?

Possible Answers:

Point C

Point B

Point E

Point D

Point F

Correct answer:

Point E

Explanation:

Alvin runs at a rate of seven miles an hour for twelve minutes, or 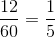$\frac{12}{60} = \frac{1}{5}$ hours. The distance he runs is equal to his rate multiplied by his time, so, setting $r = 7 , t = \frac{1}{5}$ in this formula:

d = rt

$d = 7 \cdot \frac{1}{5} = \frac{7}{5}$ miles.

One mile comprises 5,280 feet, so this is equal to

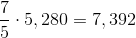
$\frac{7}{5} \cdot 5,280 = 7,392$ feet

Since each side of the track measures 264 feet, this means that Alvin runs

$7,392 \div 264 = 28$ sidelengths.

$28 \div 6 = 4 \textrm{ R }4$ ,

which means that Alvin runs around the track four complete times, plus four more sides of the track. Alvin stops when he is at Point E.

Report an Error

Example Question #2 : Hexagons

A circle with circumference 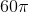$60 \pi$ is inscribed in a regular hexagon. Give the perimeter of the hexagon.

Possible Answers:

$135 \sqrt{2}$

None of these

150

$60 \sqrt{10}$

$120 \sqrt{3}$

Correct answer:

$120 \sqrt{3}$

Explanation:

Below is the figure referenced; note that the hexagon is divided by its diameters, and that an apothem—a perpendicular bisector from the center to one side—has been drawn.

Hexagon 3

The circle has circumference $C = 60 \pi$ ; its radius, which coincides with the apothem of the hexagon, is the circumference divided by $2\pi$ :

$r = \frac{C}{2\pi} = \frac{60 \pi }{2\pi} = 30$

The hexagon is divided into six equilateral triangles. One, $\bigtriangleup AOB$ , is divided by an apothem of the hexagon $\overline{OM}$ - a radius of the circle - into two 30-60-90 triangles, one of which is $\bigtriangleup AMO$ . Since $\overline{OM}$ has length 30, and it is a long leg of $\bigtriangleup AMO$ , then short leg $\overline{AM}$ has length

$AM = \frac{OM}{\sqrt{3}} = \frac{30}{\sqrt{3}} = \frac{30 \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}} =\frac{30 \sqrt{3}}{3} = 10 \sqrt{3}$

is the midpoint of $\overline{AB}$ , one of the six congruent sides of the hexagon, so

$AB = 2 \cdot AM = 2 \cdot 10 \sqrt{3} = 20\sqrt{3}$ ;

this makes the perimeter of the hexagon six times this, or

$P = 6 \cdot 20 \sqrt{3} = 120 \sqrt{3}$ .

Report an Error

View SAT Mathematics Tutors

Cole
Certified Tutor

UW Madison, Bachelors, Industrial Engineering. UW Madison, Masters, Industrial Engineering.

View SAT Mathematics Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Mathematics Tutors

Thomas
Certified Tutor

Michigan State University, Bachelor in Arts, History. Central Michigan University, Doctor of Philosophy, History.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

Spanish Courses & Classes in Washington DC, LSAT Courses & Classes in Seattle, GRE Courses & Classes in Atlanta, GMAT Courses & Classes in New York City, Spanish Courses & Classes in Houston, SSAT Courses & Classes in New York City, Spanish Courses & Classes in Phoenix, GMAT Courses & Classes in Atlanta, ACT Courses & Classes in New York City, GRE Courses & Classes in New York City

Popular Test Prep

SAT Test Prep in New York City, MCAT Test Prep in Washington DC, SSAT Test Prep in Atlanta, GMAT Test Prep in New York City, ISEE Test Prep in New York City, MCAT Test Prep in Atlanta, ACT Test Prep in New York City, ACT Test Prep in Atlanta, MCAT Test Prep in Houston, SSAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : How to find the perimeter of a hexagon

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #1 : Hexagons

Example Question #2 : Hexagons

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: