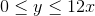Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Geometry

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #641 : Geometry

Circle a

The above circle has area $64 \pi$ . Give its equation.

Possible Answers:

$(x- 8)^{2}+ (y - 8)^2 = 8$

$(x- 32)^{2}+ (y - 32)^2 = 1,024$

$(x- 8)^{2}+ (y - 8)^2 = 64$

$\textup{None of the other choices gives the correct response}$

$(x- 32)^{2}+ (y - 32)^2 = 32$

Correct answer:

$(x- 8)^{2}+ (y - 8)^2 = 64$

Explanation:

The equation of a circle on the coordinate plane is

$(x- h)^{2}+ (y - k)^2 = r^{2}$ ,

where (h, k) are the coordinates of the center and is the radius.

The area and the radius of a circle are related by the formula

$\pi r^{2} = A$

Set $A = 64 \pi$ and solve for :

$\pi r^{2} = 64 \pi$

$\frac{ \pi r^{2} }{\pi} = \frac{64 \pi}{\pi}$

$r^{2} = 64$

$r = \sqrt{64} = 8$

As seen below, the horizontal and vertical distance from the origin to the center of the circle are both equal to this radius, and it is located in Quadrant I, so the center is (8, 8) :

Circle b

Setting h = k = r = 8 , the equation of the circle becomes

$(x- 8)^{2}+ (y - 8)^2 = 8^{2}$

$(x- 8)^{2}+ (y - 8)^2 = 64$

Report an Error

Example Question #21 : How To Find The Equation Of A Circle

Circle a

The provided circle has the following circumference:

$64 \pi$

Find its equation.

Possible Answers:

$(x- 32)^{2}+ (y - 32)^2 = 32$

$(x- 8)^{2}+ (y - 8)^2 = 8$

None of these

$(x- 8)^{2}+ (y - 8)^2 = 64$

$(x- 32)^{2}+ (y - 32)^2 = 1,024$

Correct answer:

$(x- 32)^{2}+ (y - 32)^2 = 1,024$

Explanation:

The equation of a circle on the coordinate plane is

$(x- h)^{2}+ (y - k)^2 = r^{2}$ ,

where (h, k) are the coordinates of the center and is the radius.

The radius of a circle can be determined by dividing its circumference by $2 \pi$ , so, setting $C = 64 \pi$ :

$r = \frac{C}{2 \pi } = \frac{64 \pi }{2 \pi } = 32$ .

As can be seen in the diagram below, the center of the circle is the point in Quadrant I whose horizontal and vertical distance are both equal to the radius. Therefore, both coordinates are positive - and the center therefore has center at (32, 32) .

Circle b

Setting h = k = r = 32 , the equation of the circle becomes

$(x- 32)^{2}+ (y - 32)^2 = 32^{2}$

$(x- 32)^{2}+ (y - 32)^2 = 1,024$

Report an Error

Example Question #31 : How To Find The Equation Of A Circle

Circle a

The provided figure shows a circle on the coordinate axes with its center at the origin. $\overarc {AB}$ is a $45^{\circ }$ arc with length $\frac{3}{4} \pi$

Give the equation of the circle.

Possible Answers:

$x^{2}+ y^2 =16$

$x^{2}+ y^2 =6$

$x^{2}+ y^2 =4$

$x^{2}+ y^2 =9$

$x^{2}+ y^2 =3$

Correct answer:

$x^{2}+ y^2 =9$

Explanation:

A $45^{\circ }$ arc of a circle represents $\frac{45}{360 } = \frac{1}{8}$ of the circle, so the length of the arc is one-eighth its circumference - or, equivalently, the circumference is the length $\frac{3}{4} \pi$ multiplied by 8. Therefore, the circumference is

$C = \frac{3}{4} \pi \cdot 8 = 6 \pi$ .

The equation of a circle on the coordinate plane is

$(x- h)^{2}+ (y - k)^2 = r^{2}$ ,

where (h, k) are the coordinates of the center and is the radius.

The radius of a circle can be determined by dividing its circumference by $2 \pi$ , so

$r = \frac{C}{2 \pi } = \frac{6 \pi }{2 \pi } = 3$

The center of the circle is (0,0) , so h = k = 0 . Substituting 0, 0, and 3 for , , and , respectively, the equation of the circle becomes

$(x- 0)^{2}+ (y - 0)^2 =3 ^{2}$ ,

$x^{2}+ y^2 =9$ .

Report an Error

Example Question #32 : Circles

Circle a

The provided figure shows a circle on the coordinate axes with its center at the origin. The shaded region has area $20 \pi$ .

Give the equation of the circle.

Possible Answers:

$x^{2}+ y^2 =144$

$x^{2}+ y^2 =40$

$x^{2}+ y^2 =20$

$x^{2}+ y^2 =240$

$x^{2}+ y^2 =120$

Correct answer:

$x^{2}+ y^2 =120$

Explanation:

The shaded region, a $60^{\circ }$ sector of the circle, represents $\frac{60}{360} = \frac{1}{6}$ of the circle, so the area of the entire circle is six times the area of that region:

$A = 6 \cdot 20 \pi = 120 \pi$ .

The equation of a circle on the coordinate plane is

$(x- h)^{2}+ (y - k)^2 = r^{2}$ ,

where (h, k) are the coordinates of the center and is the radius.

The formula for the area of a circle, given its radius , is

$A = \pi r ^{2}$ .

Set $A = 120 \pi$ and solve for $r^{2}$ :

$\pi r ^{2} = 120 \pi$

$\frac{\pi r ^{2} }{\pi}=\frac{ 120 \pi}{\pi}$

$r ^{2} = 120$

The center of the circle is (0,0) , so h = k = 0 . Substituting 0, 0, and 80 for , , and $r^{2}$ , respectively, the equation of the circle becomes

$(x- 0)^{2}+ (y - 0)^2 =120$

$x^{2}+ y^2 =120$

Report an Error

Example Question #32 : How To Find The Equation Of A Circle

Circle a

The provided figure shows a circle on the coordinate axes with its center at the origin. The shaded region has an area of $20 \pi$ .

Give the equation of the circle.

Possible Answers:

$x^{2}+ y^2 =20$

$x^{2}+ y^2 =80$

Cannot be determined

$x^{2}+ y^2 =40$

$x^{2}+ y^2 =160$

Correct answer:

$x^{2}+ y^2 =80$

Explanation:

The shaded region represents one fourth of the circle, so the area of the entire circle is four times the area of that region:

$4 \cdot 20 \pi = 80 \pi$ .

The equation of a circle on the coordinate plane is

$(x- h)^{2}+ (y - k)^2 = r^{2}$ ,

where (h, k) are the coordinates of the center and is the radius.

The formula for the area of a circle, given its radius , is

$A = \pi r ^{2}$ .

Set $A = 80 \pi$ and solve for $r^{2}$ :

$\pi r ^{2} = 80 \pi$

$\frac{\pi r ^{2} }{\pi}=\frac{ 80 \pi}{\pi}$

$r ^{2} = 80$

The center of the circle is (0,0) , so h = k = 0 . Substituting 0, 0, and 80 for , , and $r^{2}$ , respectively, the equation of the circle becomes

$(x- 0)^{2}+ (y - 0)^2 =80$ ,

$x^{2}+ y^2 =80$

Report an Error

Example Question #641 : Geometry

A circle is centered on point (5,12) . The area of the circle is $9\pi$ . What is the equation of the circle?

Possible Answers:

( x- 5 )^2 + ( y -12 )^2 = 9

( x -12 )^2 + ( y- 5 )^2 = 4.5

( x -5 )^2 - ( y - 12 )^2 = 9

( x -12 )^2 + ( y- 5 )^2 = 9

( x-5 )^2 + ( y -12 )^2 = 81

Correct answer:

( x- 5 )^2 + ( y -12 )^2 = 9

Explanation:

The formula for a circle is ( x -h )^2 + ( y -k )^2 = r^2

(h,k) is the coordinate of the center of the circle, therefore h = 5 and k = 12 .

The area of a circle:

$r^2\pi = 9\pi$

r^2 = 9

Therefore:

( x -h )^2 + ( y -k )^2 = r^2

( x- 5 )^2 + ( y -12 )^2 = 9

Report an Error

Example Question #1 : How To Find The Equation Of A Circle

A circle has a center at (5,5) and a radius of 2. If the format of the equation for the circle is (x-A)²+(y-B)²=C, what is C?

Possible Answers:

Correct answer:

Explanation:

The circle has a center at (5,5) and a radius of 2. Therefore, the equation is (x-5)²+(y-5)²=2², or (x-5)²+(y-5)²=4.

Report an Error

Example Question #1 : Graphing

Let D be the region on the (x,y) coordinate plane that contains the solutions to the following inequalities:

$x\leq k$ , where is a positive constant

$0\leq y\leq 12x$

Which of the following expressions, in terms of , is equivalent to the area of D?

Possible Answers:

6k^2

8k^2

12k^2

4k^2

3k^2

Correct answer:

6k^2

Explanation:

Inequality_region1

Report an Error

Example Question #1 : How To Graph A Function

Which of the following could be a value of $f(x)$ for $f(x)=-x^2 + 3$ ?

Possible Answers:

$5$

$7$

$6$

$3$

$4$

Correct answer:

$3$

Explanation:

The graph is a down-opening parabola with a maximum of $y=3$ . Therefore, there are no y values greater than this for this function.

Report an Error

Example Question #1 : How To Graph A Function

The figure above shows the graph of y = f(x). Which of the following is the graph of y = |f(x)|?

Possible Answers:

Correct answer:

Explanation:

One of the properties of taking an absolute value of a function is that the values are all made positive. The values themselves do not change; only their signs do. In this graph, none of the y-values are negative, so none of them would change. Thus the two graphs should be identical.

Report an Error

View SAT Mathematics Tutors

Amanda
Certified Tutor

Seattle University, Current Undergrad Student, Applied Mathematics.

View SAT Mathematics Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Mathematics Tutors

Irina
Certified Tutor

New York University, Bachelors, Biochemistry.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

ACT Courses & Classes in Atlanta, SAT Courses & Classes in Atlanta, LSAT Courses & Classes in Philadelphia, MCAT Courses & Classes in San Diego, GMAT Courses & Classes in Seattle, SAT Courses & Classes in New York City, GRE Courses & Classes in Chicago, SAT Courses & Classes in Houston, LSAT Courses & Classes in Los Angeles, SAT Courses & Classes in Seattle

Popular Test Prep

GMAT Test Prep in Atlanta, SAT Test Prep in Boston, MCAT Test Prep in Houston, SSAT Test Prep in Chicago, GMAT Test Prep in New York City, SSAT Test Prep in Houston, GRE Test Prep in Houston, GRE Test Prep in Chicago, GMAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Geometry

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #641 : Geometry

Example Question #21 : How To Find The Equation Of A Circle

Example Question #31 : How To Find The Equation Of A Circle

Example Question #32 : Circles

Example Question #32 : How To Find The Equation Of A Circle

Example Question #641 : Geometry

Example Question #1 : How To Find The Equation Of A Circle

Example Question #1 : Graphing

Example Question #1 : How To Graph A Function

Example Question #1 : How To Graph A Function

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: