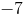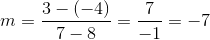Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Coordinate Geometry

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Find The Slope Of A Line

What is the slope of line 3 = 8y - 4x?

Possible Answers:

0.5

-0.5

-2

Correct answer:

0.5

Explanation:

Solve equation for y. y=mx+b, where m is the slope

Report an Error

Example Question #2 : How To Find The Slope Of A Line

Find the slope of the line 6X – 2Y = 14

Possible Answers:

-3

-6

Correct answer:

Explanation:

Put the equation in slope-intercept form:

y = mx + b

-2y = -6x +14

y = 3x – 7

The slope of the line is represented by M; therefore the slope of the line is 3.

Report an Error

Example Question #3 : How To Find The Slope Of A Line

If 2x – 4y = 10, what is the slope of the line?

Possible Answers:

–0.5

–5/2

–2

0.5

Correct answer:

0.5

Explanation:

First put the equation into slope-intercept form, solving for y: 2x – 4y = 10 → –4y = –2x + 10 → y = 1/2*x – 5/2. So the slope is 1/2.

Report an Error

Example Question #1 : How To Find Slope Of A Line

What is the slope of the line with equation 4x – 16y = 24?

Possible Answers:

1/4

1/8

–1/4

1/2

–1/8

Correct answer:

1/4

Explanation:

The equation of a line is:

y = mx + b, where m is the slope

4x – 16y = 24

–16y = –4x + 24

y = (–4x)/(–16) + 24/(–16)

y = (1/4)x – 1.5

Slope = 1/4

Report an Error

Example Question #11 : How To Find Slope Of A Line

What is the slope of a line which passes through coordinates $\dpi{100} \small (3,7)$ and $\dpi{100} \small (4,12)$ ?

Possible Answers:

$\dpi{100} \small 3$

$\dpi{100} \small \frac{1}{5}$

$\dpi{100} \small 2$

$\dpi{100} \small \frac{1}{2}$

$\dpi{100} \small 5$

Correct answer:

$\dpi{100} \small 5$

Explanation:

Slope is found by dividing the difference in the $\dpi{100} \small y$ -coordinates by the difference in the $\dpi{100} \small x$ -coordinates.

$\dpi{100} \small \frac{(12-7)}{(4-3)}=\frac{5}{1}=5$

Report an Error

Example Question #1 : How To Find The Slope Of A Line

What is the slope of the line represented by the equation $6y-16x=7$ ?

Possible Answers:

$\frac{7}{6}$

$6$

$16$

$-16$

$\frac{8}{3}$

Correct answer:

$\frac{8}{3}$

Explanation:

To rearrange the equation into a $y=mx+b$ format, you want to isolate the $y$ so that it is the sole variable, without a coefficient, on one side of the equation.

First, add $11x$ to both sides to get $6y=7+16x$ .

Then, divide both sides by 6 to get $y=\frac{7+16x}{6}$ .

If you divide each part of the numerator by 6, you get $y=\frac{7}{6}+\frac{16x}{6}$ . This is in a $y=b+mx$ form, and the $m$ is equal to $\frac{16}{6}$ , which is reduced down to $\frac{8}{3}$ for the correct answer.

Report an Error

Example Question #3 : How To Find The Slope Of A Line

What is the slope of the given linear equation?

2x + 4y = -7

Possible Answers:

-1/2

-2

-7/2

1/2

Correct answer:

-1/2

Explanation:

We can convert the given equation into slope-intercept form, y=mx+b, where m is the slope. We get y = (-1/2)x + (-7/2)

Report an Error

Example Question #231 : Geometry

What is the slope of the line:

$\frac{14}{3}x=\frac{1}{6}y-7$

Possible Answers:

$-\frac{1}{28}$

$\frac{1}{28}$

Correct answer:

Explanation:

First put the question in slope intercept form (y = mx + b):

–(1/6)y = –(14/3)x – 7 =>

y = 6(14/3)x – 7

y = 28x – 7.

The slope is 28.

Report an Error

Example Question #2 : How To Find The Slope Of A Line

What is the slope of a line that passes though the coordinates $(5,2)$ and $(3,1)$ ?

Possible Answers:

$-\frac{1}{2}$

$-\frac{2}{3}$

$\frac{1}{2}$

$4$

$\frac{2}{3}$

Correct answer:

$\frac{1}{2}$

Explanation:

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{1-2}{3-5}=\frac{-1}{-2}=\frac{1}{2}$

Report an Error

Example Question #3 : How To Find The Slope Of A Line

What is the slope of a line running through points (7,3) and (8,-4) ?

Possible Answers:

$\frac{7}{3}$

$-\frac{1}{7}$

Correct answer:

Explanation:

The slope is equal to the difference between the y-coordinates divided by the difference between the x-coordinates.

$m=\frac{y_2-y_1}{x_2-x_1}$

Use the give points in this formula to calculate the slope.

$m=\frac{3-(-4)}{7-8}=\frac{7}{-1}=-7$

Report an Error

View SAT Mathematics Tutors

Troy
Certified Tutor

Rice University, Bachelor in Arts, Kinesiology.

View SAT Mathematics Tutors

Kenneth
Certified Tutor

North Georgia University, Bachelors, Accounting. Brenau University, Masters, Business.

View SAT Mathematics Tutors

Daniel
Certified Tutor

Stony Brook University, Bachelors, Biology, General. SUNY College of Optometry, PHD, Optometry.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

GMAT Courses & Classes in Philadelphia, ISEE Courses & Classes in Phoenix, LSAT Courses & Classes in Atlanta, SAT Courses & Classes in San Diego, GMAT Courses & Classes in Houston, ACT Courses & Classes in Seattle, MCAT Courses & Classes in Atlanta, SAT Courses & Classes in Denver, Spanish Courses & Classes in Atlanta, GRE Courses & Classes in Dallas Fort Worth

Popular Test Prep

LSAT Test Prep in Los Angeles, GMAT Test Prep in Dallas Fort Worth, ACT Test Prep in Miami, ISEE Test Prep in Miami, SSAT Test Prep in Washington DC, GMAT Test Prep in Philadelphia, SAT Test Prep in New York City, GMAT Test Prep in Boston, LSAT Test Prep in Miami, ACT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Coordinate Geometry

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #2 : How To Find The Slope Of A Line

Example Question #2 : How To Find The Slope Of A Line

Example Question #3 : How To Find The Slope Of A Line

Example Question #1 : How To Find Slope Of A Line

Example Question #11 : How To Find Slope Of A Line

Example Question #1 : How To Find The Slope Of A Line

Example Question #3 : How To Find The Slope Of A Line

Example Question #231 : Geometry

Example Question #2 : How To Find The Slope Of A Line

Example Question #3 : How To Find The Slope Of A Line

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: