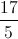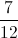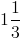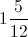Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Mixed / Improper Fractions

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Mixed / Improper Fractions

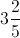
What is $3\frac{2}{5}$ as an improper fraction?

Possible Answers:

$\frac{21}{5}$

$\frac{11}{5}$

$\frac{17}{5}$

$\frac{10}{2}$

$\frac{6}{2}$

Correct answer:

$\frac{17}{5}$

Explanation:

$3\frac{2}{5}$ becomes $3 + \frac{2}{5} = \frac{15}{5} + \frac{2}{5} = \frac{17}{5}$

Report an Error

Example Question #1 : How To Find Out An Improper Fraction From A Mixed Fraction

Write $71\frac{5}{7}$ as an improper fraction.

Possible Answers:

$\frac{502}{7}$

$\frac{360}{7}$

$\frac{76}{7}$

$\frac{76}{8}$

$\frac{355}{7}$

Correct answer:

$\frac{502}{7}$

Explanation:

To find the improper fraction value, we must effectively add together 71 and ⁵/₇. To do this, we will give 71 a denominator of 7; therefore, we are transforming ⁷¹/₁ to ^x/₇. The shortest way to do this is to multiply by ⁷/₇ (which really is 1); therefore, 71 = 71 * (⁷/₇) = ⁴⁹⁷/₇.

Now add them: ^{(497 + 5)}/₇ = ⁵⁰²/₇

Report an Error

Example Question #2 : How To Find Out An Improper Fraction From A Mixed Fraction

Which of the following improper fractions is equivalent to $14\frac{2}{5}$ ?

Possible Answers:

$\frac{24}{5}$

$\frac{70}{5}$

$\frac{84}{3}$

$\frac{72}{5}$

$\frac{16}{5}$

Correct answer:

$\frac{72}{5}$

Explanation:

To find an improper fraction, you need to multiply the whole number that you have by the denominator of the associated fraction. For our problem, this means that you will multiply by , getting . Next, you add this to the numerator of your fraction, giving you 70+2 , or . Finally, you place this over your original denominator, giving you:

$\frac{72}{5}$

Report an Error

Example Question #2 : How To Find Out An Improper Fraction From A Mixed Fraction

Which of the following improper fractions is equivalent to $27\frac{4}{19}$ ?

Possible Answers:

$\frac{517}{19}$

$\frac{49}{19}$

$\frac{813}{17}$

$\frac{481}{19}$

$\frac{31}{19}$

Correct answer:

$\frac{517}{19}$

Explanation:

To find an improper fraction, you need to multiply the whole number that you have by the denominator of the associated fraction. For our problem, this means that you will multiply by , getting 513 . Next, you add this to the numerator of your fraction, giving you 513+4 , or 517 . Finally, you place this over your original denominator, giving you:

$\frac{517}{19}$

Report an Error

Example Question #1 : Mixed / Improper Fractions

To make 48 cookies you need 1 cup white sugar, 1 cup packed brown sugar and 3 cups of flour. You want to make 12 cookies, so you adjust the ingredients accordingly. After the adjustment, how many total cups of dry ingredients do you have?

Possible Answers:

³/₄ c

1 ¹/₄ c

1 ¹/₂ c

¹/₄ c

1 ³/₄ c

Correct answer:

1 ¹/₄ c

Explanation:

Going from 48 cookies to 12 cookies is a scaling factor of ¹/₄, so all the ingredients get multiplied by ¹/₄. In order to make 12 cookies you will need ¹/₄ c white sugar, 1/4 c packed brown sugar, and ³/₄ c flour. Added all together you get ⁵/₄ or 1 ¹/₄ c.

Report an Error

Example Question #2 : Mixed / Improper Fractions

What is $\frac{17}{12}$ written as a mixed number?

Possible Answers:

$1\frac{1}{3}$

$1\frac{5}{12}$

$3\frac{1}{2}$

$2\frac{1}{6}$

$\frac{7}{12}$

Correct answer:

$1\frac{5}{12}$

Explanation:

How many times does 12 go into 17? Once with a remainder of 5.

So $\frac{17}{12}$ becomes $1\frac{5}{12}$

Report an Error

Example Question #2 : Mixed / Improper Fractions

Which of the following is the mixed fraction equivalent to $\frac{19}{3}$ ?

Possible Answers:

$\frac{13}{3}$

$6\frac{3}{5}$

$\frac{3}{19}$

$6\frac{1}{3}$

$8\frac{2}{3}$

Correct answer:

$6\frac{1}{3}$

Explanation:

To begin, notice that using your calculator, you can find:

$\frac{19}{3} = 6.33333...$

Now, the closest even multiple of that is less than is . Therefore, you know that your number is:

$\frac{19}{3}=\frac{18}{3}+\frac{1}{3}$

This is the same as:

$6+\frac{1}{3}$ , or simply, $6\frac{1}{3}$ . This is your mixed fraction.

Report an Error

Example Question #3 : Mixed / Improper Fractions

Which of the following is equivalent to $\frac{82}{4}$ ?

Possible Answers:

$15\frac{3}{4}$

$20\frac{1}{2}$

$15\frac{1}{2}$

$20\frac{3}{8}$

$20\frac{1}{4}$

Correct answer:

$20\frac{1}{2}$

Explanation:

Although there are many ways to convert improper fractions into mixed fractions, the easiest way is to use your calculator to your advantage. Begin by dividing by . This gives you 20.5 . Therefore, you can eliminate all the options that have do not have for their first portion. Next, multiply 0.5 by the denominator (), and get . This means that you have and $\frac{2}{4}$ , or $\frac{1}{2}$ . Thus, your answer is $20\frac{1}{2}$ .

Report an Error

Example Question #4 : How To Find Out A Mixed Fraction From An Improper Fraction

Convert $3\frac{3}{5}$ to an improper fraction.

Possible Answers:

$\frac{18}{5}$

$\frac{5}{13}$

$\frac{5}{18}$

$\frac{11}{5}$

$\frac{13}{5}$

Correct answer:

$\frac{18}{5}$

Explanation:

The denominator will stay the same. The new numerator of the improper fraction can be determined by multiplying the denominator with the whole number coefficient, and then adding the numerator.

$3\frac{3}{5}=\frac{(5\times3)+3}{5}=\frac{18}{5}$

Report an Error

Example Question #4 : Mixed / Improper Fractions

Change $\frac{12}{7}$ into a mixed fraction.

Possible Answers:

$1\frac{6}{7}$

$1\frac{2}{7}$

$1\frac{7}{12}$

$1\frac{5}{12}$

$1\frac{5}{7}$

Correct answer:

$1\frac{5}{7}$

Explanation:

Divide 12 by 7. This means that seven goes into twelve one time. One times seven gives you seven. From here we subtract seven from twelve which give us our remainder of five.

$12\div7 = 1 \textup{ Remainder }5$

The remainder of five is a fraction of seven.

Write the mixed fraction.

The answer is:

$1\frac{5}{7}$

Report an Error

View SAT Mathematics Tutors

Cole
Certified Tutor

UW Madison, Bachelors, Industrial Engineering. UW Madison, Masters, Industrial Engineering.

View SAT Mathematics Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Mathematics Tutors

Thomas
Certified Tutor

Michigan State University, Bachelor in Arts, History. Central Michigan University, Doctor of Philosophy, History.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

LSAT Courses & Classes in Philadelphia, ACT Courses & Classes in Los Angeles, GMAT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Philadelphia, Spanish Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Chicago, ACT Courses & Classes in Atlanta, MCAT Courses & Classes in Miami, SAT Courses & Classes in Boston, MCAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

SAT Test Prep in Denver, ACT Test Prep in Philadelphia, SSAT Test Prep in Chicago, SAT Test Prep in San Diego, LSAT Test Prep in Boston, SSAT Test Prep in Boston, GRE Test Prep in Los Angeles, MCAT Test Prep in Atlanta, GRE Test Prep in Boston, ISEE Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Mixed / Improper Fractions

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #1 : Mixed / Improper Fractions

Example Question #1 : How To Find Out An Improper Fraction From A Mixed Fraction

Example Question #2 : How To Find Out An Improper Fraction From A Mixed Fraction

Example Question #2 : How To Find Out An Improper Fraction From A Mixed Fraction

Example Question #1 : Mixed / Improper Fractions

Example Question #2 : Mixed / Improper Fractions

Example Question #2 : Mixed / Improper Fractions

Example Question #3 : Mixed / Improper Fractions

Example Question #4 : How To Find Out A Mixed Fraction From An Improper Fraction

Example Question #4 : Mixed / Improper Fractions

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: