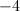Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Linear / Rational / Variable Equations

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #111 : Equations / Inequalities

Give the solution set of the rational equation $\frac{(x- 5)^{2}}{(x- 4) ^{2}} = 1$

Possible Answers:

$\left \{ - \frac{1}{2}, \frac{9}{2} \right \}$

$\left \{ 5\right \}$

$\left \{ - \frac{9}{2}, \frac{9}{2} \right \}$

$\left \{ \frac{9}{2} \right \}$

$\left \{ 4, 5\right \}$

Correct answer:

$\left \{ \frac{9}{2} \right \}$

Explanation:

Multiply both sides of the equation by the denominator $(x- 4) ^{2}$ :

$\frac{(x- 5)^{2}}{(x- 4) ^{2}} \cdot (x- 4) ^{2} =1 \cdot (x- 4) ^{2}$

$(x- 5)^{2} = (x- 4) ^{2}$

Rewrite both expression using the binomial square pattern:

$x^{2} - 2 \cdot x \cdot 5+ 5^{2} = x^{2} - 2 \cdot x \cdot 4+ 4^{2}$

$x^{2} -10x + 25 = x^{2} - 8x+16$

This can be rewritten as a linear equation by subtracting $x^{2}$ from both sides:

$x^{2} -10x + 25- x^{2} = x^{2} - 8x+16 - x^{2}$

-10x + 25 = - 8x+16

Solve as a linear equation:

-10x + 25+ 8x - 25 = - 8x+16 + 8x - 25

-2x = -9

$\frac{-2x}{-2 } =\frac{ -9 }{-2}$

$x= \frac{9}{2}$

Report an Error

Example Question #111 : Linear / Rational / Variable Equations

Solve:

$\frac{10-x}{40}=-5$

Possible Answers:

x=210

x=21

x=200

x=-210

x=-200

Correct answer:

x=210

Explanation:

$\frac{10-x}{40}=-5$

Multiply by on each side

10-x=-200

Subtract on each side

-x=-210

Multiply by on each side

x=210

Report an Error

Example Question #132 : Linear / Rational / Variable Equations

Find the solution to the following equation if x = 3:

y = (4x² - 2)/(9 - x²)

Possible Answers:

no possible solution

Correct answer:

no possible solution

Explanation:

Substituting 3 in for x, you will get 0 in the denominator of the fraction. It is not possible to have 0 be the denominator for a fraction so there is no possible solution to this equation.

Report an Error

Example Question #2 : Linear / Rational / Variable Equations

Undefined_denom3

I. x = 0

II. x = –1

III. x = 1

Possible Answers:

III only

II only

I, II, and III

I only

II and III only

Correct answer:

I only

Explanation:

Undefined_denom2

Report an Error

Example Question #133 : Linear / Rational / Variable Equations

Nosol1

Possible Answers:

–3

There is no solution

–1/2

Correct answer:

There is no solution

Explanation:

Nosol2

Report an Error

Example Question #3 : Linear / Rational / Variable Equations

$\small h\left ( x\right )=\frac{28}{x+4}$

$\small \textup{For which of the following values of}\,x\,\textup{is the above function undefined?}$

Possible Answers:

$\small 4$

$\small 28$

$\small 0$

$\small -4$

None of the other answers

Correct answer:

$\small -4$

Explanation:

A fraction is considered undefined when the denominator equals 0. Set the denominator equal to zero and solve for the variable.

$\small x+4=0$

$\small x=-4$

Report an Error

Example Question #4 : How To Find Out When An Equation Has No Solution

Solve:

3(2x - 6) + 2x = 7x - 12

Possible Answers:

Correct answer:

Explanation:

First, distribute, making sure to watch for negatives.

3(2x - 6) + 2x = 7x - 12

6x - 18 + 2x = 7x - 12

Combine like terms.

8x - 18 = 7x - 12

Subtract 7x from both sides.

x - 18 = -12

Add 18 on both sides and be careful adding integers.

x = 6

Report an Error

Example Question #1 : How To Find Out When An Equation Has No Solution

Solve:

-3(2x - 5) = 9 - 6x

Possible Answers:

No Solution

$\frac{15}{9}$

Infinitely Many Solutions

Correct answer:

No Solution

Explanation:

First, distribute the to the terms inside the parentheses.

-3(2x - 5) = 9 - 6x

-6x + 15 = 9 - 6x

Add 6x to both sides.

15 = 9

This is false for any value of . Thus, there is no solution.

Report an Error

Example Question #2 : How To Find Out When An Equation Has No Solution

Solve $\left | 3-4x\right |<0$ .

Possible Answers:

$x<\frac{4}{3}$

$x>\frac{3}{4}$

$x<\frac{3}{4}$

No solutions

$x>\frac{4}{3}$

Correct answer:

No solutions

Explanation:

By definition, the absolute value of an expression can never be less than 0. Therefore, there are no solutions to the above expression.

Report an Error

Example Question #1 : How To Find Out When An Equation Has No Solution

, Screen shot 2016 02 18 at 9.31.39 am

In the above graphic, approximately determine the x values where the graph is neither increasing or decreasing.

Possible Answers:

5<x<10

-5<x<5

-10<x<10

-3<x<3

-10<x<-5

Correct answer:

-3<x<3

Explanation:

We need to find where the graph's slope is approximately zero. There is a straight line between the x values of , and . The other x values have a slope. So our final answer is -3<x<3 .

Report an Error

View SAT Mathematics Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

View SAT Mathematics Tutors

Sharif
Certified Tutor

NCCU, Bachelors, Physics and Mathematics.

View SAT Mathematics Tutors

Miriam
Certified Tutor

Washington University in St Louis, Bachelor in Arts, Biology, General.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

ISEE Courses & Classes in Los Angeles, ACT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Atlanta, LSAT Courses & Classes in Houston, LSAT Courses & Classes in San Diego, SSAT Courses & Classes in San Diego, GMAT Courses & Classes in Los Angeles, MCAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Miami, Spanish Courses & Classes in Los Angeles

Popular Test Prep

SSAT Test Prep in Seattle, LSAT Test Prep in Miami, ISEE Test Prep in Philadelphia, GRE Test Prep in San Diego, SAT Test Prep in Phoenix, ACT Test Prep in Chicago, MCAT Test Prep in New York City, GRE Test Prep in Miami, ACT Test Prep in San Francisco-Bay Area, ISEE Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Linear / Rational / Variable Equations

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #111 : Equations / Inequalities

Example Question #111 : Linear / Rational / Variable Equations

Example Question #132 : Linear / Rational / Variable Equations

Example Question #2 : Linear / Rational / Variable Equations

Example Question #133 : Linear / Rational / Variable Equations

Example Question #3 : Linear / Rational / Variable Equations

Example Question #4 : How To Find Out When An Equation Has No Solution

Example Question #1 : How To Find Out When An Equation Has No Solution

Example Question #2 : How To Find Out When An Equation Has No Solution

Example Question #1 : How To Find Out When An Equation Has No Solution

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: