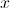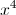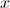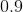If \(\displaystyle x\) is greater than 0, then adding 1 to \(\displaystyle x\) will make it greater than 1. Taking a number between 0 and 1 to a power results in a smaller number.

0.08 * 0.08

First square 8:

8 * 8 = 64

Then move the decimal four places to the left:

0.0064

The easiest way to find the square root of a fraction is to convert it into scientific notation. 

\(\displaystyle \dpi{100} \small .00081 = 8.1 \times 10^{-4}\)

The key is that the exponent in scientific notation has to be even for a square root because the square root of an exponent is diving it by two. The square root of 9 is 3, so the square root of 8.1 is a little bit less than 3, around 2.8

 \(\displaystyle \dpi{100} \small \sqrt{8.1 \times 10^{-4}} \approx 2.8 \times 10^{-2} \approx 0.028\)

To find the square root of this decimal we convert it into scientific notation.

\(\displaystyle \small 0.0049 = 49 \cdot10^{-4}\)

Because \(\displaystyle \small 10^{-4}\) has an even exponent, we can divide the exponenet by 2 to get its square root.

\(\displaystyle \small \sqrt{0.0049} = \sqrt{49}\cdot\sqrt{10^{-4}} = 7\cdot10^{-2} = 0.07\)

This problem can be solve more easily by rewriting the decimal into scientific notation.

\(\displaystyle \small 0.025 = 2.5 \times 10^{-2}\)

Because \(\displaystyle \small 10^{-2}\) has an even exponent, we can take the square root of it by dividing it by 2. The square root of 4 is 2, and the square root of 1 is 1, so the square root of 2.5 is less than 2 and greater than 1.

\(\displaystyle \small \sqrt{0.025} = \sqrt{2.5}\times \sqrt{10^{-2}} = 1.58\times 10^{-1} = 0.158\)

This problem becomes much simpler if we rewrite the decimal in scientific notation

\(\displaystyle \small 0.00036 = 3.6\times 10^{-4}\)

Because \(\displaystyle \small 10^{-4}\) has an even exponent, we can take its square root by dividing it by two. The square root of 4 is 2, and because 3.6 is a little smaller than 4, its square root is a little smaller than 2, around 1.9

\(\displaystyle \small \sqrt{0.025} = \sqrt{3.6}\times \sqrt{10^{-4}} \approx 1.9\times 10^{-2} = 0.019\)

To find the square root of this decimal we convert it into scientific notation.

\(\displaystyle \small \small 0.00064 = 6.4 \times10^{-4}\)

Because \(\displaystyle \small 10^{-4}\) has an even exponent, we can divide the exponenet by 2 to get its square root. The square root of 9 is 3, and the square root of 4 is two, so the square root of 6.4 is between 3 and 2, around 2.53

\(\displaystyle \small \small \sqrt{0.00064} = \sqrt{6.4}\times\sqrt{10^{-4}} \approx 2.53 \times10^{-2} = 0.0253\)

To find the square root of this decimal we convert it into scientific notation.

\(\displaystyle \small \small 0.0169 = 169\times10^{-4}\)

Because \(\displaystyle \small 10^{-4}\) has an even exponent, we can divide the exponenet by 2 to get its square root. \(\displaystyle \small 169\) is a perfect square, whose square root is \(\displaystyle \small 13\).

\(\displaystyle \small \small \sqrt{0.0169} = \sqrt{169}\times \sqrt{10^{-4}} =13\times10^{-2} = 0.13\)

To find the square root of this decimal we convert it into scientific notation.

\(\displaystyle \small \small \small 0.00001 = 10 \times10^{-6}\)

Because \(\displaystyle \small \small 10^{-6}\) has an even exponent, we can divide the exponenet by 2 to get its square root. The square root of 9 is 3, so the square root of 10 should be a little larger than 3, around 3.16

\(\displaystyle \small \small \sqrt{0.00001} = \sqrt{10}\times \sqrt{10^{-6}} = 3.16\times10^{-3} = 0.00316\)

To find the square root of this decimal we convert it into scientific notation.

\(\displaystyle \small \small 0.004 = 40 \times10^{-4}\)

Because \(\displaystyle \small 10^{-4}\) has an even exponent, we can divide the exponenet by 2 to get its square root. The square root of 36 is 6, so the square root of 40 should be a little more than 6, around 6.32. 

\(\displaystyle \small \small \small \sqrt{0.004} = \sqrt{40}\times\sqrt{10^{-4}} \approx 6.32 \times10^{-2} = 0.0632\)