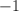We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : x and y Intercept

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : How To Find X Or Y Intercept

A line has the equation: 2x+4y=8.

What is the x-intercept?

Possible Answers:

-8

-4

Correct answer:

Explanation:

To find the x-intercept, rearrange the equation 2x+4y=8 so that x is isolated:

2x=-4y+8

x=-2y+4

Using the point-slope formula, we see that the x-intercept is 4.

Report an Error

Example Question #1 : How To Find X Or Y Intercept

What is the y intercept of the following function of x?

y = 3x

Possible Answers:

–1

–3

Correct answer:

Explanation:

The answer is 0 because in slope intercept form, y = mx + b; b is the y intercept. In this case b = 0.

Report an Error

Example Question #2 : How To Find X Or Y Intercept

What is the x-intercept of a line with a slope of 5 and y-intercept of 3.5?

Possible Answers:

(–0.7, 0)

(0, –0.7)

(–3.5, 0)

(3.5, 0)

(0.7, 0)

Correct answer:

(–0.7, 0)

Explanation:

To solve this, first find the equation of our line. The form of the question gives it to us very directly. We can use the slope-intercept form (y = mx + b).

y = 5x + 3.5

The x-intercept is found by setting y = 0, because that will give us the x-value at which the line crosses the x-axis.

0 = 5x + 3.5; –3.5 = 5x; x = –3.5 / 5 or –0.7. The point will be (–0.7, 0)

Report an Error

Example Question #4 : How To Find X Or Y Intercept

Determine the y-intercept of the following line:

$\dpi{100} \small 3x+6y=9$

Possible Answers:

$\dpi{100} \small 9$

$\dpi{100} \small 6$

$\dpi{100} \small \frac{1}{3}$

$\dpi{100} \small 1.5$

$\dpi{100} \small 3$

Correct answer:

$\dpi{100} \small 1.5$

Explanation:

The y-intercept occurs when $\dpi{100} \small x=0$

$\dpi{100} \small 3x+6y=9$

$\dpi{100} \small 3(0)+6y=9$

$\dpi{100} \small 0+6y=9$

$\dpi{100} \small y = \frac{9}{6}=1.5$

Report an Error

Example Question #161 : Psat Mathematics

At what point does the graph $3y-2x=31$ cross the -axis?

Possible Answers:

$\left ( 0,\frac{31}{3} \right )$

$\left ( 0,\frac{2}{3} \right )$

$\left ( 0,-\frac{2}{3} \right )$

$\left ( 0,\frac{3}{31} \right )$

$\left ( 0,\frac{3}{2} \right )$

Correct answer:

$\left ( 0,\frac{31}{3} \right )$

Explanation:

The graph crosses the -axis where $x=0$ . So plugging in and solving yields $\frac{31}{3}$ .

Report an Error

Example Question #162 : Geometry

Find the x-intercepts of $25x^{2}+4y^{2} = 9$ .

Possible Answers:

$\pm 5$

$5$

$\frac{3}{5}$

$2$

$\pm \frac{3}{5}$

Correct answer:

$\pm \frac{3}{5}$

Explanation:

To find the x-intercepts, plug $y=0$ into the equation and solve for $x$ .

$25x^{2} + 4\cdot 0^{2} = 9$

$25x^{2} = 9$

$x^{2} = \frac{9}{25}$

$x = \pm \frac{3}{5}$

Don't forget that there are two solutions, both negative and positive!

Report an Error

Example Question #163 : Geometry

A line with the exquation $y=x^2+3x+c$ passes through the point (-4,6) . What is the -intercept?

Possible Answers:

Correct answer:

Explanation:

By plugging in the coordinate, we can figure out that c=2 . The -Intercept is when x=0 , plugging in 0 for gives us y=2 .

Report an Error

Example Question #11 : X And Y Intercept

What are the -intercept(s) of the following line:

y=x^2+12x+27

Possible Answers:

x=-3,-9

x=27,1

x=3,9

x=3,-9

x=-3,9

Correct answer:

x=-3,-9

Explanation:

We can factor y=x^2+12x+27 and set equal to zero to determine the -intercepts.

y=(x+3)(x+9) satisfies this equation.

Therefore our -intercepts are and .

Report an Error

Example Question #171 : Coordinate Geometry

Which of the following lines does not intersect the line 4x + y = 7 ?

Possible Answers:

$y=\frac{1}{4}x-7$

$y=-\frac{1}{4}x+11$

y=4x-7

y = -4x + 5

y = 4x + 7

Correct answer:

y = -4x + 5

Explanation:

Parallel lines never intersect, so you are looking for a line that has the same slope as the one given. The slope of the given line is –4, and the slope of the line in y = –4x + 5 is –4 as well. Since these two lines have equal slopes, they will run parallel and can never intersect.

Report an Error

Example Question #172 : Coordinate Geometry

Find the y-intercept of y = 3x^2 +2x + 7 .

Possible Answers:

Correct answer:

Explanation:

To find the y-intercept, set x equal to zero and solve for y.

This gives y = 3(0)² + 2(0) +7 = 7.

Report an Error

View SAT Mathematics Tutors

Alexandra
Certified Tutor

Georgia State University, Bachelor of Fine Arts, Studio Art (Photography).

View SAT Mathematics Tutors

Bill
Certified Tutor

SUNY Empire State College, Bachelors, General Sciences, Theater.

View SAT Mathematics Tutors

Noah
Certified Tutor

Bard College, Bachelors, Philosophy and Creative Writing (Dual Major). Sarah Lawrence College, Master of Fine Arts, Creative ...

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Philadelphia, SSAT Courses & Classes in Miami, SSAT Courses & Classes in New York City, SAT Courses & Classes in San Diego, GMAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Los Angeles, SSAT Courses & Classes in Phoenix, Spanish Courses & Classes in Houston

Popular Test Prep

LSAT Test Prep in Miami, GRE Test Prep in Seattle, SSAT Test Prep in New York City, SAT Test Prep in Denver, LSAT Test Prep in Washington DC, MCAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Phoenix, ISEE Test Prep in New York City, MCAT Test Prep in Los Angeles, LSAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : x and y Intercept

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #3 : How To Find X Or Y Intercept

Example Question #1 : How To Find X Or Y Intercept

Example Question #2 : How To Find X Or Y Intercept

Example Question #4 : How To Find X Or Y Intercept

Example Question #161 : Psat Mathematics

Example Question #162 : Geometry

Example Question #163 : Geometry

Example Question #11 : X And Y Intercept

Example Question #171 : Coordinate Geometry

Example Question #172 : Coordinate Geometry

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: