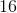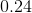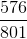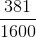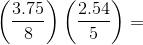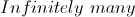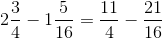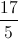All SAT Math Resources
Example Questions
Example Question #3 : Whole And Part
A pitcher of water is filled 
45
50
30
35
40
45
If 






Example Question #1 : Whole And Part
If Mr. Jones’ math class has 8 boys and two-thirds of the class are girls, how many total students are in the class?
If two-thirds of the class are girls, then one-third must be boys. Set up an equation comparing the number of boys to how much they represent in the entire class:
8 = (1/3) x, where x is the number in the entire class.
When we solve for x in the equation we get x = 24.
Example Question #121 : Fractions


With the given information, we can set up a proportion.
Example Question #1 : Decimals With Fractions
Find answer in simplified fraction form:
Multiply both the numerators or denominators by 100 to eliminate the decimals
Simplify both fractions
Multiply the numerators and multiply the denominators and simplify the fraction by dividing both the numerator and denominator by 5.
Example Question #411 : Arithmetic
If 
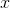
None of the other answer choices are correct
Convert all of the fractions to decimals. Thus, x is contained within the range of 0.33 < x < 0.76. The answers choices become 1/4 = 0.25, 4/12 = 0.33, 2/5 = 0.4, and 5/16 = 0.3125, respectively. Therefore, the only answer which is within the desired range is 2/5.
Example Question #1 : How To Find The Amount Of Rational Numbers Between Two Numbers
Two numbers have a greatest common divisor of 4 and a least common multiple of 40. How many different pairs of numbers are there that satisfy these properties?
The greatest common divisor is 4. This means that both numbers must be divisible by 4. Furthermore, the least common multiple is 40, so both must divide 40.
The prime factorization of 40 is 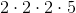
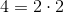
Now each number will have either two or three 2's and zero or one 5's. However, we also know that they can't both have three 2's, (since then the greatest common divisor would have three 2's as well). Similarly, only one can have a 5.
In essence, our problem becomes one of choice. We have 2 places with value 4. We choose to give a 5 to one of the two. We then give a 2 to one of the two. If we give a 5 and a 2 to the same side, we end up with 


Thus our two pairs are:
4,40 and 8,20
Example Question #1 : Compound Fractions
4/5 + 7/3 + 9/30 = ?
80 / 30
30 / 100
20 / 38
103 / 30
20 / 30
103 / 30
To add fractions you must first find the lease common denominator, that is, a number that all of the denominators (the bottom number) can divide into.
In this case, 5, 3, and 30, both 5 and 3 divide successfully into 30, so 30 is the least common denominator.
Now divide each smaller denominator into thirty. Then multiple the answer by the top number:
5/30 = 6
Therefore 4/5 = 4*6 / 5*6 = 24/30
3/30 = 10
Therefore 7*10 / 3*10 = 70/30
Then add all the numerators together:
24/30 + 70/30 +9/30 = (24+70+9)/30 = 103 / 30
Example Question #2 : Compound Fractions
The student body of a high school is 1/4 boys, and 2/3 of the boys are seniors. If 1/18 of the senior boys were accepted into Harvard, which of the following could be the total number of students in the class?
54
15
108
90
148
108
For this problem it would be easier to choose one of the answers and go from there. 108 works because 1/4 of 108 is 27 then 2/3 of 27 is 18 and 1/18 of 18 is 1, which makes this answer possible.
The other answers come out with a remainders that make no sense, since a fractional part of a person cannot have been accepted to a school.
Example Question #3 : Compound Fractions
Compute:
Rewrite each fraction into an improper fraction.
The common denominator is 16.
The correct answer is:
Example Question #1 : Mixed / Improper Fractions
What is 
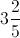
All SAT Math Resources