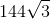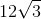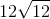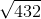We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Arithmetic

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : How To Simplify Square Roots

Simplify $(\frac{16}{81})^{1/4}$ .

Possible Answers:

$\frac{2}{3}$

$\frac{8}{81}$

$\frac{4}{9}$

$\frac{2}{81}$

$\frac{4}{81}$

Correct answer:

$\frac{2}{3}$

Explanation:

$(\frac{16}{81})^{1/4}$

$\frac{16^{1/4}}{81^{1/4}}$

$\frac{(2\cdot 2\cdot 2\cdot 2)^{1/4}}{(3\cdot 3\cdot 3\cdot 3)^{1/4}}$

$\frac{2}{3}$

Report an Error

Example Question #4 : Simplifying Square Roots

Simplfy the following radical $\sqrt{20x^{2}}$ .

Possible Answers:

$2x\sqrt{5}$

$2\sqrt{5x^{2}}$

$2x\sqrt{10}$

$4\sqrt{5x}$

Correct answer:

$2x\sqrt{5}$

Explanation:

You can rewrite the equation as $\sqrt{20x^2}=(x)\sqrt{5} \cdot \sqrt{4}$ .

This simplifies to $2x\sqrt{5}$ .

Report an Error

Example Question #1 : How To Simplify Square Roots

Which of the following is equal to $\sqrt{75}$ ?

Possible Answers:

$5\sqrt{3}$

$3\sqrt{5}$

$7.5\sqrt{10}$

Correct answer:

$5\sqrt{3}$

Explanation:

√75 can be broken down to √25 * √3. Which simplifies to 5√3.

Report an Error

Example Question #23 : Arithmetic

Simplify $\sqrt{a^{3}b^{4}c^{5}}$ .

Possible Answers:

$ab^{2}c^{2}\sqrt{ac}$

$a^{2}b^{2}c^{2}\sqrt{bc}$

$a^{2}bc^{2}\sqrt{ac}$

$a^{2}bc\sqrt{bc}$

$a^{2}b^{2}c\sqrt{ab}$

Correct answer:

$ab^{2}c^{2}\sqrt{ac}$

Explanation:

Rewrite what is under the radical in terms of perfect squares:

$x^{2}=x\cdot x$

$x^{4}=x^{2}\cdot x^{2}$

$x^{6}=x^{3}\cdot x^{3}$

Therefore, $\sqrt{a^{3}b^{4}c^{5}}= \sqrt{a^{2}a^{1}b^{4}c^{4}c^{1}}=ab^{2}c^{2}\sqrt{ac}$ .

Report an Error

Example Question #2 : Simplifying Square Roots

What is $\sqrt{50}$ ?

Possible Answers:

$2\sqrt{5}$

$10\sqrt{2}$

$5\sqrt{2}$

Correct answer:

$5\sqrt{2}$

Explanation:

We know that 25 is a factor of 50. The square root of 25 is 5. That leaves $\sqrt{2}$ which can not be simplified further.

Report an Error

Example Question #25 : Arithmetic

Which of the following is equivalent to $\frac{x + \sqrt{3}}{3x + \sqrt{2}}$ ?

Possible Answers:

$\frac{3x^{2} + \sqrt{6}}{3x - 2}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{9x^{2} - 2}$

$\frac{3x^{2} - \sqrt{6}}{9x^{2} + 2}$

$\frac{3x^{2} + 3x\sqrt{2} + x\sqrt{3} +\sqrt{6}}{9x^{2} - 2}$

$\frac{4x + \sqrt{5}}{3x + 2}$

Correct answer:

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{9x^{2} - 2}$

Explanation:

Multiply by the conjugate and the use the formula for the difference of two squares:

$\frac{x + \sqrt{3}}{3x + \sqrt{2}}$

$\frac{x + \sqrt{3}}{3x + \sqrt{2}}\cdot \frac{3x - \sqrt{2}}{3x - \sqrt{2}}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{(3x)^{2} - (\sqrt{2})^{2}}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{9x^{2} - 2}$

Report an Error

Example Question #3 : Simplifying Square Roots

Which of the following is the most simplified form of:

$\sqrt{468}$

Possible Answers:

$\sqrt{468}$

$17\sqrt{2}$

$2\sqrt{117}$

$6\sqrt{13}$

$4\sqrt{29}$

Correct answer:

$6\sqrt{13}$

Explanation:

First find all of the prime factors of 468

$468=6\ast78=6\ast6\ast13=2\ast3\ast2\ast3\ast13$

So $\sqrt{468}=\sqrt{2\ast2\ast3\ast3\ast13}=2\ast3\sqrt{13}=6\sqrt{13}$

Report an Error

Example Question #11 : How To Simplify Square Roots

What is $\sqrt{432}$ equal to?

Possible Answers:

$6\sqrt{3}$

$6\sqrt{4}$

$12\sqrt{12}$

$12\sqrt{3}$

$144\sqrt{3}$

Correct answer:

$12\sqrt{3}$

Explanation:

$\sqrt{432}$

1. We know that 432=(144)(3) , which we can separate under the square root:

$\sqrt{144\cdot 3}$

2. 144 can be taken out since it is a perfect square: $12\cdot12=144$ . This leaves us with:

$12\sqrt{3}$

This cannot be simplified any further.

Report an Error

Example Question #44 : Basic Squaring / Square Roots

Simplify: $\sqrt{240}$

Possible Answers:

$4\sqrt{15}$

$15\sqrt2$

$5\sqrt{13}$

$12\sqrt{4}$

$3\sqrt{27}$

Correct answer:

$4\sqrt{15}$

Explanation:

Write out the common square factors of the number inside the square root.

$\sqrt{240}= \sqrt{4\times 60}= 2\sqrt{60}$

Continue to find the common factors for 60.

$2\sqrt{60} = 2\sqrt{4\times 15} = 2(2\sqrt{15}) = 4\sqrt{15}$

Since there are no square factors for $\sqrt{15}$ , the answer is in its simplified form. It might not have been easy to see that 16 was a common factor of 240.

The answer is: $4\sqrt{15}$

Report an Error

Example Question #11 : How To Simplify Square Roots

Simplify:

$\sqrt{48}$

Possible Answers:

None of the given answers.

$2\sqrt{24}$

$4\sqrt{3}$

$3\sqrt{4}$

Correct answer:

$4\sqrt{3}$

Explanation:

To simplify, we want to find some factors of where at least one of the factors is a perfect square.

In this case, and are factors of , and is a perfect square.

We can simplify by saying:

$\sqrt{48} = \sqrt{16\cdot 3} = \sqrt{4^2 \cdot 3} = 4\sqrt{3}$

We could also recognize that two factors of are and . We could approach this way by saying:

$\sqrt{48}=\sqrt{4 \cdot 12} = \sqrt {2^2 \cdot 12} = 2\sqrt{12}$

But we wouldn't stop there. That's because can be further factored:

$2\sqrt{12} = 2\sqrt{4 \cdot 3} = 2\sqrt{2^2 \cdot 3} = 2\cdot 2 \sqrt{3} = 4\sqrt{3}$

Report an Error

View SAT Mathematics Tutors

Alexandra
Certified Tutor

Georgia State University, Bachelor of Fine Arts, Studio Art (Photography).

View SAT Mathematics Tutors

Bill
Certified Tutor

SUNY Empire State College, Bachelors, General Sciences, Theater.

View SAT Mathematics Tutors

Noah
Certified Tutor

Bard College, Bachelors, Philosophy and Creative Writing (Dual Major). Sarah Lawrence College, Master of Fine Arts, Creative ...

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SAT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Denver, SSAT Courses & Classes in Houston, Spanish Courses & Classes in Phoenix, MCAT Courses & Classes in Denver, ISEE Courses & Classes in Los Angeles, SSAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Miami, LSAT Courses & Classes in Boston

Popular Test Prep

SAT Test Prep in Houston, ISEE Test Prep in Denver, MCAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in New York City, ACT Test Prep in Phoenix, ISEE Test Prep in Atlanta, ACT Test Prep in Washington DC, MCAT Test Prep in Houston, SAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Arithmetic

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #3 : How To Simplify Square Roots

Example Question #4 : Simplifying Square Roots

Example Question #1 : How To Simplify Square Roots

Example Question #23 : Arithmetic

Example Question #2 : Simplifying Square Roots

Example Question #25 : Arithmetic

Example Question #3 : Simplifying Square Roots

Example Question #11 : How To Simplify Square Roots

Example Question #44 : Basic Squaring / Square Roots

Example Question #11 : How To Simplify Square Roots

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: