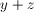Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Algebra

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #14 : Algebraic Functions

Given the functions f(x) = 2x + 4 and g(x) = 3x – 6, what is f(g(x)) when x = 6?

Possible Answers:

144

192

Correct answer:

Explanation:

We need to work from the inside to the outside, so g(6) = 3(6) – 6 = 12.

Then f(g(6)) = 2(12) + 4 = 28.

Report an Error

Example Question #15 : Algebraic Functions

A function f(x) = –1 for all values of x. Another function g(x) = 3x for all values of x. What is g(f(x)) when x = 4?

Possible Answers:

–1

–3

–12

Correct answer:

–3

Explanation:

We work from the inside out, so we start with the function f(x). f(4) = –1. Then we plug that value into g(x), so g(f(x)) = 3 * (–1) = –3.

Report an Error

Example Question #17 : Algebraic Functions

What is f(–3) if f(x) = x² + 5?

Possible Answers:

–4

–14

Correct answer:

Explanation:

f(–3) = (–3)² + 5 = 9 + 5 = 14

Report an Error

Example Question #21 : Algebraic Functions

For all values of x, f(x) = 7x² – 3, and for all values of y, g(y) = 2y + 9. What is g(f(x))?

Possible Answers:

14y² + 3

2x + 9

14x² + 3

7y² – 3

14x² – 3

Correct answer:

14x² + 3

Explanation:

The inner function f(x) is like our y-value that we plug into g(y).

g(f(x)) = 2(7x² – 3) + 9 = 14x² – 6 + 9 = 14x² + 3.

Report an Error

Example Question #22 : Algebraic Functions

Find f(6)

$f(x)=|x^{2}+4x-127|$

Possible Answers:

Correct answer:

Explanation:

Simply plug 6 into the equation and don't forget the absolute value at the end.

=36+24-127=-67

absolute value = 67

Report an Error

Example Question #41 : Algebraic Functions

An outpost has the supplies to last 2 people for 14 days. How many days will the supplies last for 7 people?

Possible Answers:

$\dpi{100} \small 9$

$\dpi{100} \small 4$

$\dpi{100} \small 7$

$\dpi{100} \small 5$

$\dpi{100} \small 10$

Correct answer:

$\dpi{100} \small 4$

Explanation:

Supplies are used at the rate of $\dpi{100} \small \frac{Supplies}{Days\times People}$ .

Since the total amount of supplies is the same in either case, $\dpi{100} \small \frac{1}{14\times 2}=\frac{1}{7\times \ (\&hash;\ of\ days)}$ .

Solve for days to find that the supplies will last for 4 days.

Report an Error

Example Question #23 : Algebraic Functions

Worker $\dpi{100} \small A$ can make a trinket in 4 hours, Worker $\dpi{100} \small B$ can make a trinket in 2 hours. When they work together, how long will it take them to make a trinket?

Possible Answers:

$\dpi{100} \small \frac{1}{2}\ hour$

$\dpi{100} \small \ 1 \frac{1}{3}\ hours$

$\dpi{100} \small 6\ hours$

$\dpi{100} \small \ 1 \frac{1}{2}\ hours$

$\dpi{100} \small 3\ hours$

Correct answer:

$\dpi{100} \small \ 1 \frac{1}{3}\ hours$

Explanation:

The rates are what needs to be added. Rate $\dpi{100} \small A$ is $\dpi{100} \small \frac{1}{4}$ , or one trinket every 4 hours. Rate $\dpi{100} \small B$ is $\dpi{100} \small \frac{1}{2}$ , one per two hours.

$\dpi{100} \small \frac{1}{4}+ \frac{1}{2}=\frac{3}{4}$ , their combined rate in trinkets per hour.

Now invert the equation to get back to hours per trinket, which is what the question asks for: $\dpi{100} \small \frac{4}{3}\ or \ 1 \frac{1}{3}$

Report an Error

Example Question #43 : Algebraic Functions

$a\ \mho \ b = a(b+1)-3$

Quantity A Quantity B

$1\ \mho\ 1$ $2\ \mho\ 0$

Possible Answers:

Quantity A and Quantity B are equal

Quantity A is greater

Quantity B is greater

The relationship cannot be determined from the information given.

Correct answer:

Quantity A and Quantity B are equal

Explanation:

Since $a\ \mho \ b = a(b+1)-3$ , then we have that

$1\ \mho \ 1=1(1+1)-3=-1$

and

$2\ \mho \ 0=2(0+1)-3=-1$ .

Thus, the two quantities are equal.

Report an Error

Example Question #44 : Algebraic Functions

If the average of two numbers is $\dpi{100} \small 3y$ and one of the numbers is $\dpi{100} \small y+z$ , what is the other number, in terms of $\dpi{100} \small y$ and $\dpi{100} \small z$ ?

Possible Answers:

$\dpi{100} \small 3y+z$

$\dpi{100} \small 5y-z$

$\dpi{100} \small 5y+z$

$\dpi{100} \small y+z$

$\dpi{100} \small 4y-z$

Correct answer:

$\dpi{100} \small 5y-z$

Explanation:

The average is the sum of the terms divided by the number of terms. Here you have $\dpi{100} \small y+z$ and the other number which you can call $\dpi{100} \small x$ . The average of $\dpi{100} \small x$ and $\dpi{100} \small y+z$ is $\dpi{100} \small 3y$ . So $\dpi{100} \small 3y=\frac{(x+y+z)}{2}$

Multiply both sides by 2.

Solve for $\dpi{100} \small x=5y-z$ .

Report an Error

Example Question #45 : Algebraic Functions

Alice is twice as old as Tom, but four years ago, she was three years older than Tom is now. How old is Tom now?

Possible Answers:

$\dpi{100} \small 13$

$\dpi{100} \small 21$

$\dpi{100} \small 3$

$\dpi{100} \small 7$

$\dpi{100} \small 9$

Correct answer:

$\dpi{100} \small 7$

Explanation:

The qustion can be broken into two equations with two unknows, Alice age $\dpi{100} \small (A)$ and Tom's age $\dpi{100} \small (T)$ .

$\dpi{100} \small A=2T$

$\dpi{100} \small A-4=T+3$

$\dpi{100} \small 2T-4=T+3$

$\dpi{100} \small T=7$

Report an Error

View SAT Mathematics Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SAT Mathematics Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

View SAT Mathematics Tutors

Daniel
Certified Tutor

Stony Brook University, Bachelors, Biology, General. SUNY College of Optometry, PHD, Optometry.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

SSAT Courses & Classes in Denver, GRE Courses & Classes in New York City, LSAT Courses & Classes in Chicago, SAT Courses & Classes in Chicago, SSAT Courses & Classes in Miami, ACT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in San Diego, Spanish Courses & Classes in Atlanta, SAT Courses & Classes in Philadelphia, Spanish Courses & Classes in Chicago

Popular Test Prep

GRE Test Prep in Miami, MCAT Test Prep in Los Angeles, SAT Test Prep in Washington DC, GRE Test Prep in New York City, GRE Test Prep in San Diego, GRE Test Prep in Dallas Fort Worth, SAT Test Prep in New York City, ISEE Test Prep in Philadelphia, MCAT Test Prep in Seattle, ISEE Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Algebra

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #14 : Algebraic Functions

Example Question #15 : Algebraic Functions

Example Question #17 : Algebraic Functions

Example Question #21 : Algebraic Functions

Example Question #22 : Algebraic Functions

Example Question #41 : Algebraic Functions

Example Question #23 : Algebraic Functions

Example Question #43 : Algebraic Functions

Example Question #44 : Algebraic Functions

Example Question #45 : Algebraic Functions

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: