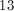All SAT Math Resources
Example Questions
Example Question #121 : Algebraic Functions
Alice is twice as old as Tom, but four years ago, she was three years older than Tom is now. How old is Tom now?
The qustion can be broken into two equations with two unknows, Alice age 

Example Question #46 : Algebraic Functions
A jet goes from City 1 to City 2 at an average speed of 600 miles per hour, and returns along the same path at an average speed if 300 miles per hour. What is the average speed, in miles per hour, for the trip?
500miles/hour
350miles/hour
400miles/hour
450miles/hour
300miles/hour
400miles/hour
Chose a number for the distance between City 1 and 2; 1800 works well, as it is a multiple of 600 and 300.
Now, find the time for each trip, the total distance, and the total time.
Now we can find the average speed by dividing the total distance by the total time.
Example Question #122 : Algebraic Functions
Find 
Plug 5 into 
Now, plug this answer into 
Example Question #123 : Algebraic Functions
If 


Plug g(x) into f(x) as if it is just a variable. This gives f(g(x)) = 3(x2 – 12) + 7.
Distribute the 3: 3x2 – 36 + 7 = 3x2 – 29
Example Question #2821 : Sat Mathematics

Some values of the function 
For which of the following values of 


If 

so 
When we try the other values for b, our g(b) does not match.
We can verify by trying the other possible answer choices as follows.
And 
Example Question #124 : Algebraic Functions
f(x) = 4x + 17
Solve f(x) for the equation above for x = 3.
26
32
19
29
12
29
The correct answer is 29. We plug in 3 into the equation above and solve for x. So we find that f(x) = 4(3) + 17. 12 + 17 = 29
Example Question #1055 : Algebra
Define a function 

If 



Therefore, solve the equation


Either 



Example Question #1056 : Algebra

Define 
Give the 


The 


From the diagram, it can be seen that 
The 


Example Question #1057 : Algebra

Define 
Give the 


The correct answer is not given among the other four responses.
The correct answer is not given among the other four responses.
The 


From the diagram, it can be seen that 




Example Question #86 : How To Find F(X)

Define 
Which of the following is an 



The graph of 

An 



or, equivalently,
or
From the diagram below, it can be seen that if 



Therefore, the graph of 



The correct choice is therefore 
All SAT Math Resources