Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math II : Trigonometry

Study concepts, example questions & explanations for SAT II Math II

Create An Account

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Sine, Cosine, Tangent

Find the value of 5tan(60) in exact form.

Possible Answers:

$10\sqrt3$

$\frac{5\sqrt{3}}{2}$

$\frac{5\sqrt{3}}{3}$

$5\sqrt{3}$

$\frac{10\sqrt3}{3}$

Correct answer:

$5\sqrt{3}$

Explanation:

Recall that:

$tan(\theta) = \frac{sin(\theta)}{cos(\theta)}$

This means that: $tan(60) = \frac{sin(60)}{cos(60)}$

$sin(60) = \frac{\sqrt3}{2}$

$cos(60) = \frac{1}{2}$

Divide the two terms.

$\frac{\sqrt3}{2} \div \frac{1}{2} = \frac{\sqrt3}{2} \times \frac{2}{1} = \sqrt3$

This means that $5tan(60) = 5\sqrt{3}$ .

The answer is: $5\sqrt{3}$

Report an Error

Example Question #1 : Sum And Difference Identities For Tangent

According to the trigonometric identities, 1+cot^2(x)=?

Possible Answers:

tan(x)

$\frac{1}{tan(x)}$

csc^2(x)

$\frac{sin(x)}{cos(x)}$

Correct answer:

csc^2(x)

Explanation:

The trigonometric identity 1+cot^2(x)=csc^2(x) , is an important identity to memorize.

Some other identities that are important to know are:

$\frac{sin(x)}{cos(x)}=tan(x)$

$cot(x)=\frac{1}{tan(x)}$

sin^2(x)+cos^2(x)=1

Report an Error

Example Question #1 : Radians And The Unit Circle

The degree angle 300 can be expressed as what in radians?

Possible Answers:

$\frac{11}{6}\pi$

$\frac{7}{6}\pi$

$\frac{4}{3}\pi$

$\frac{5}{3}\pi$

$\frac{6}{5}\pi$

Correct answer:

$\frac{5}{3}\pi$

Explanation:

In order to convert degrees to radians, we will need to know the conversion factor.

$180 \textup{ deg} = \pi \textup{ rad}$

Set up a dimensional analysis to solve.

$300 \textup{ deg} (\frac{\pi \textup{ rad}}{180 \textup{ deg}}) = \frac{5}{3}\pi\textup{ rad}$

The answer is: $\frac{5}{3}\pi$

Report an Error

Example Question #12 : Trigonometry

Which of the following angles belong in the fourth quadrant?

Possible Answers:

$\pi$

$\frac{5}{2}\pi$

$\frac{17}{9}\pi$

$\frac{4}{3}\pi$

Correct answer:

$\frac{17}{9}\pi$

Explanation:

The fourth quadrant is in the positive x-axis and negative y-axis.

The angle ranges are:

$270\rightleftharpoons 360 \textup{ deg}$

$\frac{3}{2}\pi\rightleftharpoons 2\pi \textup{ radians}$

The only possible answer is: $\frac{17}{9}\pi$

Report an Error

Example Question #1 : Radians And The Unit Circle

What degree measure is equivalent to $4\pi$ ?

Possible Answers:

540

980

360

1020

720

Correct answer:

720

Explanation:

Every pi radians is equal to 180 degrees.

Replace the pi term with 180 degrees and multiply.

$4\pi = 4(180 \textup{ degrees}) = 720$

The answer is: 720

Report an Error

Example Question #12 : Trigonometry

A triangle has sides that measure 10, 12, and 16. What is the greatest measure of any of its angles (nearest tenth of a degree)?

Possible Answers:

$131.5^{\circ}$

$141.4^{\circ}$

$120.0^{\circ}$

$92.9^{\circ}$

$87.1^{\circ}$

Correct answer:

$92.9^{\circ}$

Explanation:

We are seeking the measure of the angle opposite the side of greatest length, 16.

We can use the Law of Cosines, setting c = 16, a= 10, b = 12 , and solving for :

$\cos C = \frac{a^{2}+b^{2}- c^{2}}{2ab}$

$\cos C = \frac{10^{2}+12^{2}- 16^{2}}{2 \cdot 10 \cdot 12}$

$\cos C = \frac{100+144- 256}{240}$

$\cos C = \frac{-12}{240}$

$\cos C =- 0.0500$

$C = \cos ^{-1}(-0.0500) \approx 92.9^{\circ}$

Report an Error

Example Question #1 : Law Of Cosines

A triangle has sides that measure 15, 17, and 30. What is the least measure of any of its angles (nearest tenth of a degree)?

Possible Answers:

$19.1^{\circ}$

$68.3^{\circ}$

$70.9^{\circ}$

$21.7^{\circ}$

$67.8^{\circ}$

Correct answer:

$19.1^{\circ}$

Explanation:

We are seeking the measure of the angle opposite the side of least length, 15.

We can use the Law of Cosines, setting c = 15, a= 17, b = 30 , and solving for :

$\cos C = \frac{a^{2}+b^{2}- c^{2}}{2ab}$

$\cos C = \frac{17^{2}+30^{2}- 15^{2}}{2 \cdot 17 \cdot 30}$

$\cos C = \frac{289+900- 225 }{1,020}$

$\cos C = \frac{964 }{1,020}$

$\cos C \approx 0.9451$

$C \approx \cos ^{-1} 0.9451 \approx 19.1^{\circ}$

Report an Error

Example Question #13 : Trigonometry

Given : $\Delta ABC$ with $AB = 12, BC = 17, m \angle B= 136 ^{\circ}$ .

Which of the following whole numbers is closest to ?

Possible Answers:

Correct answer:

Explanation:

Apply the Law of Cosines

$c =\sqrt{ a^{2}+b^{2}- 2ab \cos C}$

setting $a = 12, b= 17, C= 136 ^{\circ}$ and solving for :

$c =\sqrt{ 12^{2}+17^{2}- 2\cdot 12 \cdot 17 \cos 136^{\circ}}$

$c \approx \sqrt{144+289-408 (-0.7193)}$

$c \approx \sqrt{144+289+293.49}$

$c \approx \sqrt{726.49}$

$c \approx 27.0$

Of the five choices, 27 comes closest.

Report an Error

Example Question #4 : Law Of Cosines

Given : $\Delta ABC$ with $AB = 12, BC = 16, m \angle B= 56 ^{\circ}$ .

Evaluate to the nearest tenth.

Possible Answers:

9.0

14.7

13.6

13.0

The correct answer is not given among the other responses.

Correct answer:

13.6

Explanation:

Apply the Law of Cosines

$c =\sqrt{ a^{2}+b^{2}- 2ab \cos C}$

setting $a = 12, b = 16, C = 56^{\circ}$ and solving for :

$c =\sqrt{ 12^{2}+16^{2}- 2\cdot 12 \cdot 16 \cos 56^{\circ}}$

$c \approx \sqrt{ 144+256- 384 \cdot 0.5592 }$

$c \approx \sqrt{ 144+256- 214.73 }$

$c \approx \sqrt{ 185.27 }$

$c \approx 13.6$

Report an Error

Example Question #5 : Law Of Cosines

In $\bigtriangleup ABC$ :

AB = 12

AC = 15

$m \angle A = 105^{\circ }$

Evaluate the length of $\overline{BC}$ to the nearest tenth of a unit.

Possible Answers:

19.2

21.6

21.2

16.6

26.8

Correct answer:

21.6

Explanation:

The figure referenced is below:

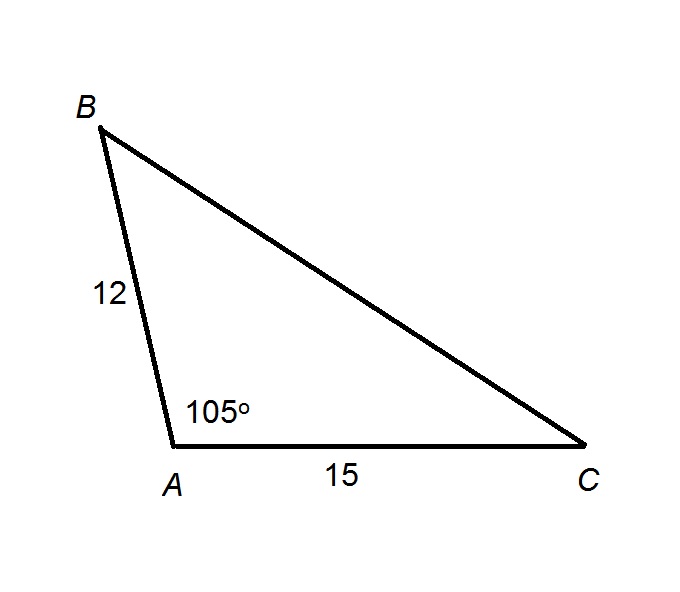
Triangle 2

By the Law of Cosines, given the lengths and of two sides of a triangle, and the measure $\gamma$ of their included angle, the length of the third side can be calculated using the formula

$c^{2} = a ^{2} + b^{2} - 2ab \cos \gamma$

Substituting a = AB = 12 , b = AC = 15 , c = BC , and $\gamma = m \angle A = 105^{\circ }$ , then evaluating:

$(BC)^{2} = 12^{2} + 15 ^{2} - 2 (12)(15)\cos 105^{\circ }$

$\approx 144+225 - 360 (-0.2588 )$

$\approx 369 - (-93.17 )$

$\approx 462.17$

Taking the square root of both sides:

$BC\approx \sqrt{462.17} \approx 21.6$

Report an Error

View SAT Subject Test in Mathematics Level 2 Tutors

Gordon
Certified Tutor

Arizona State University, Bachelor of Science, Biological and Physical Sciences.

View SAT Subject Test in Mathematics Level 2 Tutors

Stephen
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor of Science, Geophysics and Seismology.

View SAT Subject Test in Mathematics Level 2 Tutors

Dwarka
Certified Tutor

Birla Institute of Technology Science, Bachelors, Electronics Engg. Case Western Reserve University, Masters, Computer Engg;...

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Atlanta, SAT Tutors in Philadelphia, French Tutors in Houston, LSAT Tutors in Los Angeles, SSAT Tutors in Houston, ACT Tutors in Los Angeles, Reading Tutors in Phoenix, Biology Tutors in Washington DC, LSAT Tutors in Boston, ISEE Tutors in Boston

Popular Courses & Classes

GRE Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Denver, SSAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Los Angeles, Spanish Courses & Classes in Philadelphia, SSAT Courses & Classes in Los Angeles, SAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in New York City, ISEE Courses & Classes in San Diego

Popular Test Prep

GMAT Test Prep in Chicago, GMAT Test Prep in New York City, LSAT Test Prep in Chicago, GRE Test Prep in Boston, LSAT Test Prep in Boston, SSAT Test Prep in Dallas Fort Worth, GRE Test Prep in Dallas Fort Worth, SAT Test Prep in Phoenix, SAT Test Prep in Philadelphia, ACT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math II : Trigonometry

Study concepts, example questions & explanations for SAT II Math II

All SAT II Math II Resources

Example Questions

Example Question #1 : Sine, Cosine, Tangent

Example Question #1 : Sum And Difference Identities For Tangent

Example Question #1 : Radians And The Unit Circle

Example Question #12 : Trigonometry

Example Question #1 : Radians And The Unit Circle

Example Question #12 : Trigonometry

Example Question #1 : Law Of Cosines

Example Question #13 : Trigonometry

Example Question #4 : Law Of Cosines

Example Question #5 : Law Of Cosines

All SAT II Math II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: