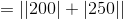SAT II Math II : Number Theory
Study concepts, example questions & explanations for SAT II Math II
All SAT II Math II Resources
Example Questions
Example Question #1 : Number Theory
Express 
Place values in the base two system are powers of two rather than powers of ten.
Example Question #1 : Number Theory
Express 68 as a base two (binary) number.
68 can be expressed as the sum of distinct powers of two as follows:
Therefore, there are 1's in the seventh and third place from the right, and 0's everywhere else, so
Example Question #1 : Sat Subject Test In Math Ii
Express 73 as a binary (base two) number.
73 can be uniquely expressed as the sum of distinct powers of two as follows:
Therefore, there is a "1" in the seventh, fourth, and first positions from the right, and a "0" everywhere else. So,
Example Question #2 : Sat Subject Test In Math Ii
Which of the following numbers is an imaginary number?
By definition, an imaginary number is a number with the term "i" in it. For this problem 7i is the only answer with the imaginary part.
Example Question #1 : Number Theory
Define an operation 
For any two real numbers 
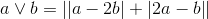
Evaluate 
Substitute 
Example Question #2 : Number Theory
The above represents a Venn diagram. The universal set 
Let 
As you can see, the three sets divide the universal set into eight regions. Suppose each positive integer was placed in the correct region. Which of the following numbers would be in the same region as 873?
From the last digit, it can be immediately determined that 873 is not a multple of 2 or 5; since 
We are looking for an integer that is also in this set - that is, one that is also a multiple of 3 but not 2 or 5. From the last digits, we can immediately eliminate 366 and 368 as multiples of 2 and 365 as a multiple of 5. We test 367 and 369 to see which one is a multiple of 3:
369 is the correct choice.
Example Question #3 : Number Theory
Which of the following sets is closed under multiplication?
A set is closed under multiplication if and only if the product of any two (not necessarily distinct) elements of that set is itself an element of that set.
This can easily be disproved in the case of three of these sets:
But closure can be proved to hold in the case of 
which is an element of 
Example Question #3 : Number Theory
What is the power set for the data set?
The power set is the set of all subsets that can be created from the original set.
For the set 
This means that the power set is the set of all sets, so the power set is:
Example Question #2 : Number Theory
Multiply:
None of the other responses is correct.
None of the other responses is correct.
This is the product of a complex number and its complex conjugate. They can be multiplied using the pattern
with
This is not among the given responses.
Example Question #4 : Number Theory
Multiply:
None of the other responses is correct.
All SAT II Math II Resources
