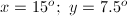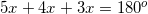We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math II : 2-Dimensional Geometry

Study concepts, example questions & explanations for SAT II Math II

Create An Account

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #352 : Sat Subject Test In Math Ii

Regular Pentagon ABCDE has perimeter 35. $\overline{AB }$ has as its midpoint; segment $\overline{ME}$ is drawn. To the nearest tenth, give the length of $\overline{ME}$ .

Possible Answers:

14.4

11.3

8.7

9.2

8.2

Correct answer:

8.7

Explanation:

The perimeter of the regular pentagon is 35, so each side measures one fifth of this, or 7. Also, since is the midpoint of $\overline{AB}$ , $AM = BM = \frac{1}{2}AB = \frac{1}{2} \cdot 7= 3.5$ .

Also, each interior angle of a regular pentagon measures $108^{\circ }$ .

Below is the pentagon in question, with indicated and $\overline{ME}$ constructed; all relevant measures are marked.

Pentagon 1

A triangle $\bigtriangleup MBC$ is formed with AM = 3.5 , AE= 7 , and included angle measure $\angle A= 108^{\circ }$ . The length of the remaining side can be calculated using the law of cosines:

$c^{2} = a^{2} + b^{2} -2 ab \cos \gamma$

where and are the lengths of two sides, $\gamma$ is the measure of their included angle, and is the length of the third side.

Setting $a = AM = 3.5, b=AE= 7, \gamma= m \angle A = 108^{\circ }$ , and c = ME , substitute and evaluate :

$(ME)^{2} = 3.5 ^{2} + 7^{2} -2 (3.5) (7) \cos 108^{\circ }$

$\approx 12.25 + 49 -49(-0.3090)$

$\approx 61.25 + 15.14$

$(ME)^{2} \approx 76.39$ ;

Taking the square root of both sides:

$ME \approx\sqrt{ 76.39 } \approx 8.7$ ,

the correct choice.

Report an Error

Example Question #51 : Geometry

Regular Hexagon ABCDEF has perimeter 360. $\overline{AF}$ and $\overline{DE}$ have and as midpoints, respectively; segment $\overline{MN}$ is drawn. To the nearest tenth, give the length of $\overline{MN}$ .

Possible Answers:

79.5

94.6

72.4

120.0

90.0

Correct answer:

90.0

Explanation:

The perimeter of the regular hexagon is 360, so each side measures one sixth of this, or 60. Since is the midpoint of $\overline{AB}$ , $AM = MF = \frac{1}{2}AF= \frac{1}{2} \cdot 60 = 30$ .

Similarly, DN = NE = 30 .

Also, each interior angle of a regular hexagon measures $120 ^{\circ }$ .

Below is the hexagon with the midpoints and , and with $\overline{MN}$ constructed. Note that perpendiculars have been drawn to $\overline{MN}$ from and , with feet at points and respectively.

Hexagon

EFXY is a rectangle, so XY = EF= 60 .

$m \angle MBX = m \angle MBC- m \angle XBC = 120 ^{\circ } - 90 ^{\circ } = 30 ^{\circ }$ .

This makes $\overline{MX}$ and $\overline{MF}$ the short leg and hypotenuse of a 30-60-90 triangle; as a consequence,

$MX = \frac{1}{2} \cdot MF = \frac{1}{2} \cdot 30 = 15$ .

For the same reason,

YN = 1 5

Adding the segment lengths:

MN = MX + XY + NY = 15 + 60 + 15 = 90 .

Report an Error

Example Question #4 : Finding Sides

Regular Pentagon ABCDE has perimeter 60.

To the nearest tenth, give the length of diagonal $\overline{BD}$ .

Possible Answers:

11.6

15.7

19.4

15 .0

14.1

Correct answer:

19.4

Explanation:

The perimeter of the regular pentagon is 60, so each side measures one fifth of this, or 12. Also, each interior angle of a regular pentagon measures $108^{\circ }$ .

The pentagon, along with diagonal $\overline{BD}$ , is shown below:

Pentagon 2

A triangle $\bigtriangleup BCD$ is formed with AB=BC = 16 , and included angle measure $\angle B= 108^{\circ }$ . The length of the remaining side can be calculated using the Law of Cosines:

$c^{2} = a^{2} + b^{2} -2 ab \cos \gamma$

where and are the lengths of two sides, $\gamma$ the measure of their included angle, and the length of the side opposite that angle.

Setting $a = BC= 12 , b= CD = 12, \gamma = m \angle C = 108^{\circ }$ , and c= BD , substitute and evaluate :

$(BD)^{2} = 12 ^{2} + 12 ^{2} -2 (12) (12) \cos 108^{\circ }$

$\approx 144+144 -288 (-0.3090)$

$\approx 288 + 89.00$

$(BD)^{2} \approx 377.00$

Taking the square root of both sides:

$BD\approx\sqrt{ 377.00 } \approx 19.4$ ,

the correct choice.

Report an Error

Example Question #51 : 2 Dimensional Geometry

Given a cube, if the volume is 100 feet cubed, what must be the side?

Possible Answers:

$10\sqrt[3]{3}$

$\sqrt[3]{100}$

$\sqrt{\frac{100}{3}}$

$10\sqrt3$

Correct answer:

$\sqrt[3]{100}$

Explanation:

Write the formula for the volume of the cube.

V=s^3

To solve for , cube root both sides.

$\sqrt[3]{V}=\sqrt[3]{s^3}$

$s=\sqrt[3]{V}$

Substitute the volume.

The answer is: $\sqrt[3]{100}$

Report an Error

Example Question #1 : Angles

Solve for and .

(Figure not drawn to scale).

Possible Answers:

$\small x=15^o;\ y=52.5^o$

$\small x=15^o;\ y=37.5^o$

$\small x=7.5^o;\ y=18.75^o$

$\small x=15^o;\ y=7.5^o$

Correct answer:

$\small x=15^o;\ y=37.5^o$

Explanation:

The angles containing the variable all reside along one line, therefore, their sum must be 180^o .

$\small 5x+4x+3x=180^o$

$\small 12x=180^o$

$\small x=15^o$

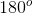
Because and are opposite angles, they must be equal.

$\small 2y=5x$

$\small x=15^o$

$\small 2y=5(15^o)=75^o$

$\small y=\frac{75^o}{2}=37.5^o$

Report an Error

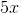
Example Question #2 : Finding Angles

What angle do the minute and hour hands of a clock form at 6:15?

Possible Answers:

$95^{\circ }$

$97 \frac{1}{2}^{\circ }$

$90^{\circ }$

$87 \frac{1}{2}^{\circ }$

$92 \frac{1}{2}^{\circ }$

Correct answer:

$97 \frac{1}{2}^{\circ }$

Explanation:

There are twelve numbers on a clock; from one to the next, a hand rotates $\left (\frac{360}{12} \right )^{\circ } = 30^{\circ }$ . At 6:15, the minute hand is exactly on the "3" - that is, on the $\left (30 \times 3 \right )^{\circ }= 90^{\circ }$ position. The hour hand is one-fourth of the way from the "6" to the "7" - that is, on the $\left (6 \frac{1}{4} \times 30 \right )^{\circ } = 187 \frac{1}{2} ^{\circ }$ position. Therefore, the difference is the angle they make:

$187 \frac{1}{2} ^{\circ } - 90^{\circ } = 97 \frac{1}{2}^{\circ }$ .

Report an Error

Example Question #2 : Finding Angles

In triangle $\Delta ABC$ , $m\angle A = 50^{\circ }$ and $m \angle B = 80^{\circ }$ . Which of the following describes the triangle?

Possible Answers:

$\Delta ABC$ is acute and isosceles.

$\Delta ABC$ is obtuse and scalene.

None of the other responses is correct.

$\Delta ABC$ is acute and scalene.

$\Delta ABC$ is obtuse and isosceles.

Correct answer:

$\Delta ABC$ is acute and isosceles.

Explanation:

Since the measures of the three interior angles of a triangle must total $180^{\circ }$ ,

$m \angle C + m \angle A + m \angle B = 180^{\circ }$

$m \angle C + 50^{\circ } + 80^{\circ } = 180^{\circ }$

$m \angle C + 130^{\circ } = 180^{\circ }$

$m \angle C = 50^{\circ }$

All three angles have measure less than $90^{\circ }$ , making the triangle acute. Also, by the Isosceles Triangle Theorem, since $m \angle A= m \angle C = 50^{\circ }$ , BC = AB ; the triangle has two congruent sides and is isosceles.

Report an Error

Example Question #1 : Finding Angles

In $\Delta DEF$ , $\angle D$ and $\angle E$ are complementary, and $m\angle D > m \angle E$ . Which of the following is true of $\Delta DEF$ ?

Possible Answers:

None of the other responses is correct.

$\Delta DEF$ is right and isosceles.

$\Delta DEF$ is right and scalene.

$\Delta DEF$ is acute and scalene.

$\Delta DEF$ is acute and isosceles.

Correct answer:

$\Delta DEF$ is right and scalene.

Explanation:

$\angle D$ and $\angle E$ are complementary, so, by definition, $m\angle D + m\angle E = 90^{\circ }$ .

Since the measures of the three interior angles of a triangle must total $180^{\circ }$ ,

$m \angle F + m \angle D + m \angle E = 180^{\circ }$

$m \angle F + 90^{\circ } = 180^{\circ }$

$m \angle F = 90^{\circ }$

$\angle F$ is a right angle, so $\Delta DEF$ is a right triangle.

$\angle D$ and $\angle E$ must be acute, so neither is congruent to $\angle F$ ; also, $\angle D$ and $\angle E$ are not congruent to each other. Therefore, all three angles have different measure. Consequently, all three sides have different measure, and $\Delta DEF$ is scalene.

Report an Error

Example Question #2 : Finding Angles

Decagon

The above figure is a regular decagon. Evaluate $m \angle ACB$ .

Possible Answers:

$24^{\circ }$

$18^{\circ }$

$15^{\circ }$

$20^{\circ }$

$12^{\circ }$

Correct answer:

$18^{\circ }$

Explanation:

As an interior angle of a regular decagon, $\angle B$ measures

$m \angle B = \left [\frac{180(10-2)}{10} \right ] ^{\circ }= 144^{\circ }$ .

Since $\overline{AB}$ and $\overline{BC}$ are two sides of a regular polygon, they are congruent. Therefore, by the Isosceles Triangle Theorem,

$m \angle ACB = m \angle CAB$

The sum of the measures of a triangle is $180^{\circ }$ , so

$m \angle ACB + m \angle CAB + m \angle ABC =180^{\circ }$

$m \angle ACB + m \angle ACB + 144 ^{\circ } =180^{\circ }$

$2 m \angle ACB + 144 ^{\circ } =180^{\circ }$

$2 m \angle ACB =36^{\circ }$

$m \angle ACB =18^{\circ }$

Report an Error

Example Question #1 : Finding Angles

Hexagon

The above hexagon is regular. What is ?

Possible Answers:

x = 64

x = 69

x = 74

None of the other responses is correct.

x = 79

Correct answer:

x = 79

Explanation:

Two of the angles of the quadrilateral formed are angles of a regular hexagon, so each measures

$\frac{180^{\circ } (6-2)}{6}= 120^{\circ }$ .

The four angles of the quadrilateral are $120 ^{\circ }, 120^{\circ }, 41^{\circ }, x^{\circ }$ . Their sum is $360^{\circ }$ , so we can set up, and solve for in, the equation:

x + 120 + 120 + 41 =360

x + 281 =360

x = 79

Report an Error

View SAT Subject Test in Mathematics Level 2 Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View SAT Subject Test in Mathematics Level 2 Tutors

Reza
Certified Tutor

University of Sherbrooke, Doctor of Philosophy, Mathematics. University of Manitoba, Master of Science, Mathematics.

View SAT Subject Test in Mathematics Level 2 Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Phoenix, MCAT Tutors in Philadelphia, French Tutors in Chicago, French Tutors in Phoenix, MCAT Tutors in Chicago, Statistics Tutors in Houston, ISEE Tutors in Miami, English Tutors in Denver, Reading Tutors in Dallas Fort Worth, SSAT Tutors in Chicago

Popular Courses & Classes

GMAT Courses & Classes in Chicago, MCAT Courses & Classes in San Diego, LSAT Courses & Classes in Atlanta, ACT Courses & Classes in Denver, GMAT Courses & Classes in Phoenix, MCAT Courses & Classes in Chicago, GRE Courses & Classes in New York City, GRE Courses & Classes in Philadelphia, MCAT Courses & Classes in Phoenix, GRE Courses & Classes in San Francisco-Bay Area

Popular Test Prep

MCAT Test Prep in New York City, SSAT Test Prep in Houston, MCAT Test Prep in Boston, LSAT Test Prep in Washington DC, MCAT Test Prep in Atlanta, SSAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Denver, GRE Test Prep in New York City, GMAT Test Prep in Phoenix, SSAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math II : 2-Dimensional Geometry

Study concepts, example questions & explanations for SAT II Math II

All SAT II Math II Resources

Example Questions

Example Question #352 : Sat Subject Test In Math Ii

Example Question #51 : Geometry

Example Question #4 : Finding Sides

Example Question #51 : 2 Dimensional Geometry

Example Question #1 : Angles

Example Question #2 : Finding Angles

Example Question #2 : Finding Angles

Example Question #1 : Finding Angles

Example Question #2 : Finding Angles

Example Question #1 : Finding Angles

All SAT II Math II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: