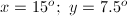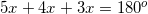We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math II : Finding Angles

Study concepts, example questions & explanations for SAT II Math II

Create An Account

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Angles

Solve for and .

(Figure not drawn to scale).

Possible Answers:

$\small x=15^o;\ y=52.5^o$

$\small x=15^o;\ y=37.5^o$

$\small x=7.5^o;\ y=18.75^o$

$\small x=15^o;\ y=7.5^o$

Correct answer:

$\small x=15^o;\ y=37.5^o$

Explanation:

The angles containing the variable all reside along one line, therefore, their sum must be 180^o .

$\small 5x+4x+3x=180^o$

$\small 12x=180^o$

$\small x=15^o$

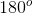
Because and are opposite angles, they must be equal.

$\small 2y=5x$

$\small x=15^o$

$\small 2y=5(15^o)=75^o$

$\small y=\frac{75^o}{2}=37.5^o$

Report an Error

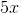
Example Question #2 : Finding Angles

What angle do the minute and hour hands of a clock form at 6:15?

Possible Answers:

$95^{\circ }$

$97 \frac{1}{2}^{\circ }$

$90^{\circ }$

$87 \frac{1}{2}^{\circ }$

$92 \frac{1}{2}^{\circ }$

Correct answer:

$97 \frac{1}{2}^{\circ }$

Explanation:

There are twelve numbers on a clock; from one to the next, a hand rotates $\left (\frac{360}{12} \right )^{\circ } = 30^{\circ }$ . At 6:15, the minute hand is exactly on the "3" - that is, on the $\left (30 \times 3 \right )^{\circ }= 90^{\circ }$ position. The hour hand is one-fourth of the way from the "6" to the "7" - that is, on the $\left (6 \frac{1}{4} \times 30 \right )^{\circ } = 187 \frac{1}{2} ^{\circ }$ position. Therefore, the difference is the angle they make:

$187 \frac{1}{2} ^{\circ } - 90^{\circ } = 97 \frac{1}{2}^{\circ }$ .

Report an Error

Example Question #2 : Finding Angles

In triangle $\Delta ABC$ , $m\angle A = 50^{\circ }$ and $m \angle B = 80^{\circ }$ . Which of the following describes the triangle?

Possible Answers:

$\Delta ABC$ is acute and isosceles.

$\Delta ABC$ is obtuse and scalene.

None of the other responses is correct.

$\Delta ABC$ is acute and scalene.

$\Delta ABC$ is obtuse and isosceles.

Correct answer:

$\Delta ABC$ is acute and isosceles.

Explanation:

Since the measures of the three interior angles of a triangle must total $180^{\circ }$ ,

$m \angle C + m \angle A + m \angle B = 180^{\circ }$

$m \angle C + 50^{\circ } + 80^{\circ } = 180^{\circ }$

$m \angle C + 130^{\circ } = 180^{\circ }$

$m \angle C = 50^{\circ }$

All three angles have measure less than $90^{\circ }$ , making the triangle acute. Also, by the Isosceles Triangle Theorem, since $m \angle A= m \angle C = 50^{\circ }$ , BC = AB ; the triangle has two congruent sides and is isosceles.

Report an Error

Example Question #1 : Finding Angles

In $\Delta DEF$ , $\angle D$ and $\angle E$ are complementary, and $m\angle D > m \angle E$ . Which of the following is true of $\Delta DEF$ ?

Possible Answers:

None of the other responses is correct.

$\Delta DEF$ is right and isosceles.

$\Delta DEF$ is right and scalene.

$\Delta DEF$ is acute and scalene.

$\Delta DEF$ is acute and isosceles.

Correct answer:

$\Delta DEF$ is right and scalene.

Explanation:

$\angle D$ and $\angle E$ are complementary, so, by definition, $m\angle D + m\angle E = 90^{\circ }$ .

Since the measures of the three interior angles of a triangle must total $180^{\circ }$ ,

$m \angle F + m \angle D + m \angle E = 180^{\circ }$

$m \angle F + 90^{\circ } = 180^{\circ }$

$m \angle F = 90^{\circ }$

$\angle F$ is a right angle, so $\Delta DEF$ is a right triangle.

$\angle D$ and $\angle E$ must be acute, so neither is congruent to $\angle F$ ; also, $\angle D$ and $\angle E$ are not congruent to each other. Therefore, all three angles have different measure. Consequently, all three sides have different measure, and $\Delta DEF$ is scalene.

Report an Error

Example Question #2 : Finding Angles

Decagon

The above figure is a regular decagon. Evaluate $m \angle ACB$ .

Possible Answers:

$24^{\circ }$

$18^{\circ }$

$15^{\circ }$

$20^{\circ }$

$12^{\circ }$

Correct answer:

$18^{\circ }$

Explanation:

As an interior angle of a regular decagon, $\angle B$ measures

$m \angle B = \left [\frac{180(10-2)}{10} \right ] ^{\circ }= 144^{\circ }$ .

Since $\overline{AB}$ and $\overline{BC}$ are two sides of a regular polygon, they are congruent. Therefore, by the Isosceles Triangle Theorem,

$m \angle ACB = m \angle CAB$

The sum of the measures of a triangle is $180^{\circ }$ , so

$m \angle ACB + m \angle CAB + m \angle ABC =180^{\circ }$

$m \angle ACB + m \angle ACB + 144 ^{\circ } =180^{\circ }$

$2 m \angle ACB + 144 ^{\circ } =180^{\circ }$

$2 m \angle ACB =36^{\circ }$

$m \angle ACB =18^{\circ }$

Report an Error

Example Question #1 : Finding Angles

Hexagon

The above hexagon is regular. What is ?

Possible Answers:

x = 64

x = 69

x = 74

None of the other responses is correct.

x = 79

Correct answer:

x = 79

Explanation:

Two of the angles of the quadrilateral formed are angles of a regular hexagon, so each measures

$\frac{180^{\circ } (6-2)}{6}= 120^{\circ }$ .

The four angles of the quadrilateral are $120 ^{\circ }, 120^{\circ }, 41^{\circ }, x^{\circ }$ . Their sum is $360^{\circ }$ , so we can set up, and solve for in, the equation:

x + 120 + 120 + 41 =360

x + 281 =360

x = 79

Report an Error

Example Question #2 : Finding Angles

What angle do the minute and hour hands of a clock form at 4:15?

Possible Answers:

$27\frac{1}{2} ^{\circ }$

$32\frac{1}{2} ^{\circ }$

$40 ^{\circ }$

$37\frac{1}{2} ^{\circ }$

$30 ^{\circ }$

Correct answer:

$37\frac{1}{2} ^{\circ }$

Explanation:

There are twelve numbers on a clock; from one to the next, a hand rotates $\left (\frac{360}{12} \right )^{\circ } = 30^{\circ }$ . At 4:15, the minute hand is exactly on the "3" - that is, on the $\left (30 \times 3 \right )^{\circ }= 90^{\circ }$ position. The hour hand is one-fourth of the way from the "4" to the "5" - that is, on the $\left (4 \frac{1}{4} \times 30 \right )^{\circ } = 127 \frac{1}{2} ^{\circ }$ position. Therefore, the difference is the angle they make:

$127 \frac{1}{2} ^{\circ } - 90^{\circ } = 37 \frac{1}{2}^{\circ }$ .

Report an Error

Example Question #1 : Finding Angles

If the vertical angles of intersecting lines are: 2x-9 and 3x+6 , what must be the value of ?

Possible Answers:

$\frac{93}{5}$

$\frac{183}{5}$

Correct answer:

Explanation:

Vertical angles of intersecting lines are always equal.

Set the two expressions equal to each other and solve for .

2x-9 = 3x+6

Subtract from both sides.

2x-9 -2x= 3x+6-2x

-9 = x+6

Subtract 6 from both sides.

-9 -6= x+6-6

The answer is:

Report an Error

Example Question #3 : Finding Angles

If the angles in degrees are x+3 and x+7 which are complementary to each other, what is three times the value of the smallest angle?

Possible Answers:

129

255

120

264

141

Correct answer:

129

Explanation:

Complementary angles add up to 90 degrees.

Set up an equation such that the sum of both angles equal to 90.

x+3+x+7 = 90

2x+10 = 90

Subtract 10 from both sides.

2x+10 -10= 90-10

2x=80

Divide by 2 on both sides.

$\frac{2x}{2}=\frac{80}{2}$

x=40

The angles are:

x+3 = 40+3 = 43

x+7 = 40+7 = 47

Three times the value of the smallest angle is:

$43\times 3 = 129$

The answer is: 129

Report an Error

Example Question #1 : Finding Angles

If the angles -10x-5 and are supplementary, what must be the value of ?

Possible Answers:

$\frac{37}{3}$

$-\frac{37}{3}$

Correct answer:

Explanation:

Supplementary angles sum up to 180 degrees.

-10x-5+5x = 180

-5x-5 = 180

Add five on both sides.

-5x-5 +5= 180+5

-5x = 185

Divide by negative five on both sides to determine .

$\frac{-5x}{-5} = \frac{185}{-5}$

x=-37

The answer is:

Report an Error

View SAT Subject Test in Mathematics Level 2 Tutors

Shakeel
Certified Tutor

View SAT Subject Test in Mathematics Level 2 Tutors

Evgenii
Certified Tutor

View SAT Subject Test in Mathematics Level 2 Tutors

Nate
Certified Tutor

University of Wisconsin-Oshkosh, non degree, Prepharmacy. University of Wisconsin-Madison, Pharmaceutical Chemist, Pharmacy.

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Philadelphia, ISEE Tutors in Phoenix, GRE Tutors in Chicago, SSAT Tutors in Philadelphia, Chemistry Tutors in Houston, French Tutors in New York City, Math Tutors in Philadelphia, Calculus Tutors in San Francisco-Bay Area, SSAT Tutors in Chicago, SSAT Tutors in Atlanta

Popular Courses & Classes

LSAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Atlanta, Spanish Courses & Classes in San Diego, MCAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Atlanta, SSAT Courses & Classes in San Diego, MCAT Courses & Classes in New York City, GMAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Boston, ISEE Courses & Classes in Dallas Fort Worth

Popular Test Prep

MCAT Test Prep in Seattle, ACT Test Prep in Los Angeles, SAT Test Prep in Seattle, MCAT Test Prep in Philadelphia, GMAT Test Prep in Los Angeles, GRE Test Prep in Los Angeles, GMAT Test Prep in Dallas Fort Worth, SSAT Test Prep in New York City, GRE Test Prep in Boston, GMAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math II : Finding Angles

Study concepts, example questions & explanations for SAT II Math II

All SAT II Math II Resources

Example Questions

Example Question #1 : Angles

Example Question #2 : Finding Angles

Example Question #2 : Finding Angles

Example Question #1 : Finding Angles

Example Question #2 : Finding Angles

Example Question #1 : Finding Angles

Example Question #2 : Finding Angles

Example Question #1 : Finding Angles

Example Question #3 : Finding Angles

Example Question #1 : Finding Angles

All SAT II Math II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: