Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math II : Circles, Ellipses, and Hyperbolas

Study concepts, example questions & explanations for SAT II Math II

Create An Account

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Coordinate Geometry

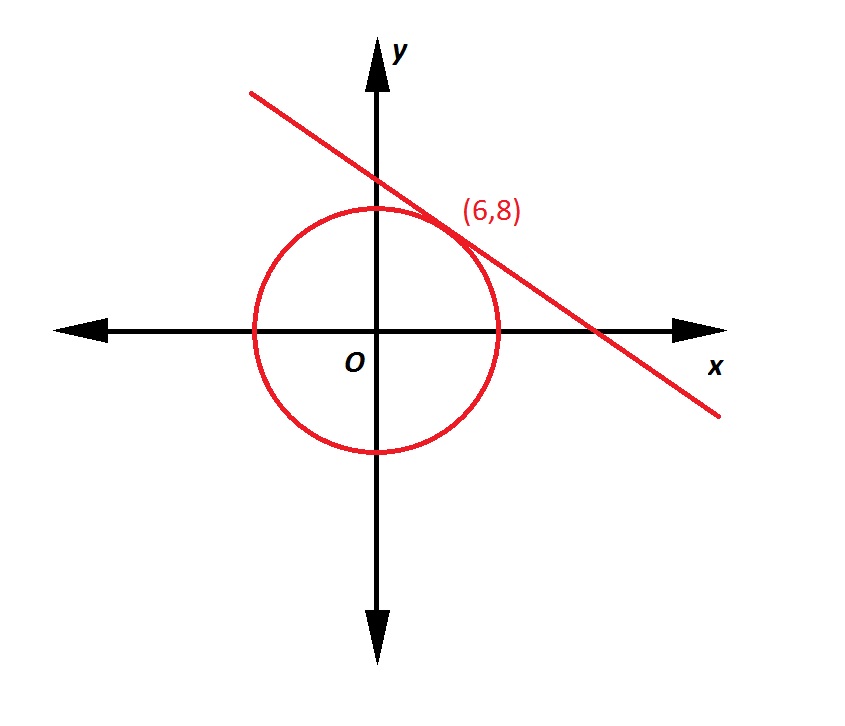
Circle

Refer to the above figure. The circle has its center at the origin. What is the equation of the circle?

Possible Answers:

$\frac{x^{2}}{36}- \frac{y^{2} }{64}= 1$

$x^{2}+ y^{2} = 100$

$x^{2}+ y^{2} = 1 0$

$\frac{y^{2} }{64 } - \frac{x^{2}}{36} = 1$

$\frac{x^{2}}{36}+ \frac{y^{2} }{64}= 1$

Correct answer:

$x^{2}+ y^{2} = 100$

Explanation:

The equation of a circle with center (h, k) and radius is

$(x-h)^{2}+ \left ( y - k\right )^{2} = r^{2}$

The center is at the origin, or (0,0) , so h = k = 0 . To find $r^{2}$ , use the distance formula as follows:

$r^{2} = \left ( 6-0\right )^{2} +\left ( 8 -0 \right )^{2} = 6^{2}+8^{2} = 36 + 64 = 100$

Note that we do not actually need to find .

We can now write the equation of the circle:

$(x-0)^{2}+ \left ( y - 0\right )^{2} = 100$

$x^{2}+y^{2} = 100$

Report an Error

Example Question #1 : Circles, Ellipses, And Hyperbolas

Circle

Refer to the above diagram. The circle has its center at the origin; is the point (-9, -12) . What is the length of the arc $\widehat{AB}$ , to the nearest tenth?

Possible Answers:

18.8

37.5

33.2

56.8

16.6

Correct answer:

33.2

Explanation:

First, it is necessary to determine the radius of the circle. This is the distance between (0,0) and (-9, -12) , so we apply the distance formula:

$r = \sqrt{(x_{2} - x _{1})^{2}+(y_{2} - y_{1})^{2}}$

$r = \sqrt{\left ( -9-0\right )^{2} +\left ( -12 -0 \right )^{2} }$

$r=\sqrt{ (-9)^{2}+(-12)^{2}}$

$r= \sqrt{81+144 }= \sqrt{225} = 15$

The circumference of the circle is

$C = 2 \pi r = 2 \pi \cdot 15 = 30 \pi$

Now we need to find the degree measure of the arc. We can do this best by examining this diagram:

Circle

The degree measure of $\widehat{AB}$ is also the measure $\theta$ of the central angle formed by the green radii. This is found using the relationship

$\tan \theta = \frac{y}{x}$

$\tan \theta = \frac{-12}{-9} \approx 1.333$

Using a calculator, we find that $\tan ^{-1} 1.3333 \approx 53.12^{\circ }$ . We can adjust for the location of :

$\theta \approx \left (180 - 53.12 \right )^{\circ } \approx 126.87^{\circ }$

which is the degree measure of the arc.

Now we can calculate the length of the arc:

$L \approx \frac{126.87}{360} \cdot C$

$L \approx \frac{126.87}{360} \cdot 30 \pi \approx 33.2$

Report an Error

Example Question #1 : Coordinate Geometry

On the coordinate plane, the vertices of a square are at the points with coordinates (7, 0), (0, 7), (-7, 0) , (0, -7) . Give the equation of the circle.

Possible Answers:

$(x- 7) ^{2}+ (y- 7) ^{2}= \frac{49}{4}$

$x^{2}+ y^{2}= \frac{7}{2}$

$x^{2}+ y^{2}= \frac{49}{4}$

$(x- 7) ^{2}+ (y- 7) ^{2}= \frac{7}{2}$

$x^{2}+ y^{2}= \frac{49}{2}$

Correct answer:

$x^{2}+ y^{2}= \frac{49}{2}$

Explanation:

The figure in question is below.

Incircle 1

The center of the circle can be seen to be the origin, so, if the radius is , the equation will be

$x^{2}+ y^{2} = r^{2}$ .

The circle passes through the midpoints of the sides, so we will find one of these midpoints. The midpoint $(x_{m}, y_{m})$ of the segment with endpoints (7,0) and (0, 7) can be found by using the midpoint equations, setting $x_{1} = y_{2}= 7, x_{2} = y_{1}= 0$ :

$x_{m} = \frac{x_{1}+x_{2}}{2} = \frac{7+0}{2} = \frac{7}{2}$

$y_{m} = \frac{y_{1}+y_{2}}{2} = \frac{0+7 }{2} = \frac{7}{2}$

The circle passed though this midpoint $\left ( \frac{7}{2}, \frac{7}{2} \right )$ . The segment from this point to the origin (0,0) is a radius, and its length is equal to . Using the following form of the distance formula, since we only need the square of the radius:

$r ^{2} = (x_{2}-x_{1}) ^{2} + (y_{2}-y_{1}) ^{2}$ ,

set $x_{1} = y_{1} = 0, x_{2}= y_{2}= \frac{7}{2}$ :

$r ^{2} =\left (\frac{7}{2}-0\right ) ^{2}+\left (\frac{7}{2}-0\right ) ^{2}$

$=\left (\frac{7}{2} \right ) ^{2}+\left (\frac{7}{2}\right ) ^{2}$

$= \frac{49}{4} + \frac{49}{4}$

$= \frac{49}{2}$

Substituting in the circle equation for $r ^{2}$ , we get the correct response,

$x^{2}+ y^{2}= \frac{49}{2}$

Report an Error

Example Question #1 : Circles, Ellipses, And Hyperbolas

Find the diameter of the circle with the equation x^2-10x+y^2+2y+10=0 .

Possible Answers:

Correct answer:

Explanation:

Start by putting the equation in the standard form of the equation of a circle by completing the square. Recall the standard form of the equation of a circle:

(x-a)^2+(y-b)^2=r^2 , where the center of the circle is at (a,b) and the radius is .

x^2-10x+25+y^2+2y+1+10=25+1

(x-5)^2+(y+1)^2+10=26

(x-5)^2+(y+1)^2=16

From the equation, we know that r^2=16 .

$r=\sqrt{16}=4$

Since the radius is , double its length to find the length of the diameter. The length of the diameter is .

Report an Error

Example Question #1 : Circles, Ellipses, And Hyperbolas

A triangle has its vertices at the points with coordinates (0,0) , (4, 4) , and (7, 0 ) . Give the equation of the circle that circumscribes it.

Possible Answers:

$x^{2}+y^{2}-7x-y=0$

$x^{2}+y^{2}-7x-15 y=0$

$x^{2}+ y^{2}+7x -15y = 0$

$x^{2}+y^{2}+7x-y=0$

None of these

Correct answer:

$x^{2}+y^{2}-7x-y=0$

Explanation:

The circumscribed circle of a triangle is the circle which passes through all three vertices of the triangle.

In general form, the equation of a circle is

$x^{2}+ y^{2}+ Ax + By + C = 0$ .

Since the circle passes through the origin, substitute x = 0, y = 0 ; the equation becomes

$0^{2}+0^{2}+ A \cdot 0 + B \cdot 0 + C = 0$

0+0+0+0 + C = 0

C= 0

Therefore, we know the equation of any circle passing through the origin takes the form

$x^{2}+ y^{2}+ Ax + By = 0$

for some A , B .

Since the circle passes through (7,0) , substitute x = 7, y = 0 ; the equation becomes

$7^{2}+ 0^{2}+ A \cdot 7 + B \cdot 0 = 0$

49+7A= 0

Solving for :

7A = -49

A = -7

Now we know that the equation takes the form

$x^{2}+ y^{2}-7x + By = 0$

for some .

Since the circle passes through (4, 4) , substitute x = 7, y = 0 ; the equation becomes

$4^{2}+ 4^{2}- 7 \cdot 4 + B \cdot 4 = 0$

16+16- 28 + 4B = 0

4 + 4B = 0

Solving for :

4B = -4

B = -1

The general form of the equation of the circle is therefore

$x^{2}+ y^{2}-7x -y = 0$

Report an Error

View SAT Subject Test in Mathematics Level 2 Tutors

Bryson
Certified Tutor

Western Oregon University, Bachelor of Science, Social Science Teacher Education. Lewis Clark College, Master of Arts Teachi...

View SAT Subject Test in Mathematics Level 2 Tutors

Barry
Certified Tutor

CUNY Lehman College, Bachelors, Math. CUNY Lehman College, Masters, Math Education.

View SAT Subject Test in Mathematics Level 2 Tutors

Christopher
Certified Tutor

Arizona State University, Bachelor of Science, Mathematics.

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Houston, Math Tutors in Miami, ACT Tutors in Los Angeles, Algebra Tutors in Phoenix, GMAT Tutors in Atlanta, ACT Tutors in Dallas Fort Worth, LSAT Tutors in Philadelphia, Algebra Tutors in New York City, Chemistry Tutors in Philadelphia, GRE Tutors in Atlanta

Popular Courses & Classes

Spanish Courses & Classes in Seattle, LSAT Courses & Classes in Philadelphia, ACT Courses & Classes in Boston, ACT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Chicago, MCAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Phoenix, SAT Courses & Classes in Los Angeles

Popular Test Prep

SAT Test Prep in Denver, SAT Test Prep in Atlanta, SAT Test Prep in Chicago, MCAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in New York City, SSAT Test Prep in Philadelphia, ISEE Test Prep in San Diego, GRE Test Prep in Washington DC, ACT Test Prep in Boston, ACT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math II : Circles, Ellipses, and Hyperbolas

Study concepts, example questions & explanations for SAT II Math II

All SAT II Math II Resources

Example Questions

Example Question #1 : Coordinate Geometry

Example Question #1 : Circles, Ellipses, And Hyperbolas

Example Question #1 : Coordinate Geometry

Example Question #1 : Circles, Ellipses, And Hyperbolas

Example Question #1 : Circles, Ellipses, And Hyperbolas

All SAT II Math II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: