Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : Surface Area

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #771 : Geometry

The radius of the base of a cone is ; its slant height is two-thirds of the diameter of that base. Give its surface area in terms of .

Possible Answers:

$\frac{\left (6- \sqrt{7} \right )\pi r ^{2}}{3}$

$\frac{5\pi r ^{2}}{3}$

$\frac{7\pi r ^{2}}{3}$

$\frac{\left (3- \sqrt{5} \right )\pi r ^{2}}{3}$

$\frac{4\pi r ^{2}}{3}$

Correct answer:

$\frac{7\pi r ^{2}}{3}$

Explanation:

The formula for the surface area of a cone with base of radius and slant height is

$A = \pi r^{2} + \pi r l$ .

The diameter of the base is twice radius , or , and its slant height is two-thirds of this diameter, which is $\frac{2}{3}\cdot 2r = \frac{4}{3}r$ . Substitute this for in the formula:

$A = \pi r^{2} + \pi r \cdot \frac{4}{3}r$

$A = \pi r^{2} + \frac{4}{3} \pi r ^{2}$

$A = \frac{7}{3} \pi r ^{2} = \frac{7\pi r ^{2}}{3}$

Report an Error

Example Question #2 : How To Find The Surface Area Of A Cone

The radius of the base of a cone is ; its height is twice of the diameter of that base. Give its surface area in terms of .

Possible Answers:

$3 \pi r^{2}$

$5 \pi r^{2}$

$\left ( 1+ \sqrt{5} \right ) \pi r^{2}$

$\left ( 1+2 \sqrt{5} \right ) \pi r^{2}$

$\left ( 1+ \sqrt{17} \right ) \pi r^{2}$

Correct answer:

$\left ( 1+ \sqrt{17} \right ) \pi r^{2}$

Explanation:

The formula for the surface area of a cone with base of radius and slant height is

$A = \pi r^{2} + \pi r l$ .

The base has radius and diameter . The height is twice the diamter, which is . Its slant height can be calculated using the Pythagorean Theorem:

$l = \sqrt{r^{2}+ h^{2}}$

$l = \sqrt{r^{2}+ (4r)^{2}}$

$l = \sqrt{r^{2}+ 16r^{2}}$

$l = \sqrt{17r^{2}}$

$l = r \sqrt{17 }$

Substitute $r \sqrt{17 }$ for in the surface area formula:

$A = \pi r^{2} + \pi r \cdot r \sqrt{17}$

$A = \pi r^{2} + \pi r^{2} \sqrt{17}$

$A = \left ( 1+ \sqrt{17} \right ) \pi r^{2}$

Report an Error

Example Question #16 : Solid Geometry

The height of a cone is ; the diameter of its base is twice the height. Give its surface area in terms of .

Possible Answers:

$10 \pi h^{2}$

$4 \pi h^{2}$

$5 \pi h^{2}$

$\left (2 +2 \sqrt{2} \right ) \pi h^{2}$

$\left (1 + \sqrt{2} \right ) \pi h^{2}$

Correct answer:

$\left (1 + \sqrt{2} \right ) \pi h^{2}$

Explanation:

The formula for the surface area of a cone with base of radius and slant height is

$A = \pi r^{2} + \pi r l$ .

The diameter of the base is twice the height, which is ; the radius is half this, which is .

The slant height can be calculated using the Pythagorean Theorem:

$l = \sqrt{r^{2}+ h^{2}}$

$l = \sqrt{h^{2}+ h^{2}}$

$l = \sqrt{2h^{2}}$

$l =h \sqrt{2}$

Substitute $h \sqrt{2}$ for and for in the surface area formula:

$A = \pi h^{2} + \pi h \cdot h \sqrt{2}$

$A = \pi h^{2} + \pi h ^{2} \sqrt{2}$

$A = \left (1 + \sqrt{2} \right ) \pi h^{2}$

Report an Error

Example Question #123 : Geometry

The circumference of the base of a cone is 80; the slant height of the cone is equal to twice the diameter of the base. Give the surface area of the cone (nearest whole number).

Possible Answers:

2,039

2,485

2,546

4,077

1,975

Correct answer:

2,546

Explanation:

The formula for the surface area of a cone with base of radius and slant height is

$A = \pi r^{2} + \pi r l$ .

The slant height is twice the diameter, or, equivalently, four times the radius, so

l = 4r

and

$A = \pi r^{2} + \pi r \cdot 4r$

$A = \pi r^{2} +4 \pi r^{2}$

$A = 5 \pi r^{2}$

The radius of the base is the circumference divided by $2\pi$ , which is

$80 \div 2 \pi \approx 80 \div (2 \times 3.14 )\approx 12.73$

Substitute:

$A = 5 \pi r^{2}$

$A \approx 5 \cdot 3.14 \cdot (12.73)^{2}$

$A \approx 2,546$

Report an Error

Example Question #2 : How To Find The Surface Area Of A Cone

The circumference of the base of a cone is 100; the height of the cone is equal to the diameter of the base. Give the surface area of the cone (nearest whole number).

Possible Answers:

2,575

2,385

1,779

8,443

1,589

Correct answer:

2,575

Explanation:

The formula for the surface area of a cone with base of radius and slant height is

$A = \pi r^{2} + \pi r l$ .

The diameter of the base is the circumference divided by $\pi$ , which is

$d = C \div (2\pi ) \approx 100 \div 3.14 \approx 31.83$

This is also the height .

The radius is half this, or

$r = d \div 2 \approx 31.83 \div 2 \approx 15.92$

The slant height can be found by way of the Pythagorean Theorem:

$l = \sqrt{r^{2}+ h ^{2}}$

$l \approx \sqrt{15.92^{2}+ 31.83 ^{2}}$

$l \approx \sqrt{253.30+ 1,013.21}$

$l \approx \sqrt{1266.51}$

$l \approx 35.60$

Substitute in the surface area formula:

$A = \pi r^{2} + \pi r l$

$A \approx 3.14 \cdot 15.92 ^{2} + 3.14 \cdot 15.92 \cdot 35.60$

$A \approx 795.8+ 1,780.1$

$A \approx 2,575$

Report an Error

Example Question #21 : Surface Area

If a cone were unfurled into a 2-dimensional figure. The lateral area of the cone would look most like which figure?

Possible Answers:

Rectangle

Sector of a Circle

Triangle

Circle

Correct answer:

Sector of a Circle

Explanation:

When creating a net image of a 3D figure - one imagines it is made of paper and is unfurled into its' 2D form. The lateral portion of the cone cone would be unfurled into the image of a Sector of a Circle. To include the full surface area of the cone a circle is included to form the base of the cone as in the figure below. The lateral area portion is the top part of the figure below.

Cone net

Report an Error

Example Question #22 : Surface Area

Find the surface area of a cube with side length of 6in.

Possible Answers:

250cm^2

18cm^2

36cm^2

24cm^2

216cm^2

Correct answer:

216cm^2

Explanation:

A cube is made up of 6 identical sides. Find the area of one side and multiplying it by 6 will result in the surface area of a cube.

S=6a^2

a is the side length, in this case 6in.

S=6(6cm)^2=6*36cm^2=216cm^2

Report an Error

Example Question #27 : Surface Area

What is the surface area of a cylinder with height 10 and radius 7?

Possible Answers:

$238\pi$

$163\pi$

$140\pi$

$300\pi$

$98\pi$

Correct answer:

$238\pi$

Explanation:

The formula of the surface area of a cylinder is:

$SA=2\pi rh+2\pi r^2$

In this problem h is 10 and r is 7. Substituting in those values gives us:

$SA=2\pi 7*10+2\pi 7^2$

Simplifying and combining the like terms results in:

$SA=140\pi+98\pi=238\pi$

Report an Error

Example Question #28 : Surface Area

Figure not drawn to scale.

Box example

Find the surface area of the box above.

Possible Answers:

Surface area: 48 yd²

Surface area: 84 yd²

Surface area: 82 yd³

Surface area: 84 yd³

Surface area: 82 yd²

Correct answer:

Surface area: 82 yd²

Explanation:

Box example

You can find the surface area of a box by following the equation below:

$\small \small \small Surface Area = 2(length\times height) + 2(length\times depth) + 2(height\times depth)$

$\small \small \small 2(7\times 3) + 2(7\times 2) + 2(3\times 2)=$

$\small 2(21) + 2(14) + 2(6)=$

$\small \small 42 + 28 + 12= 82$

The surface area of the box is 82yd²(remember that area measurements are square units NOT cubic units)

Report an Error

Example Question #29 : Surface Area

Box 3

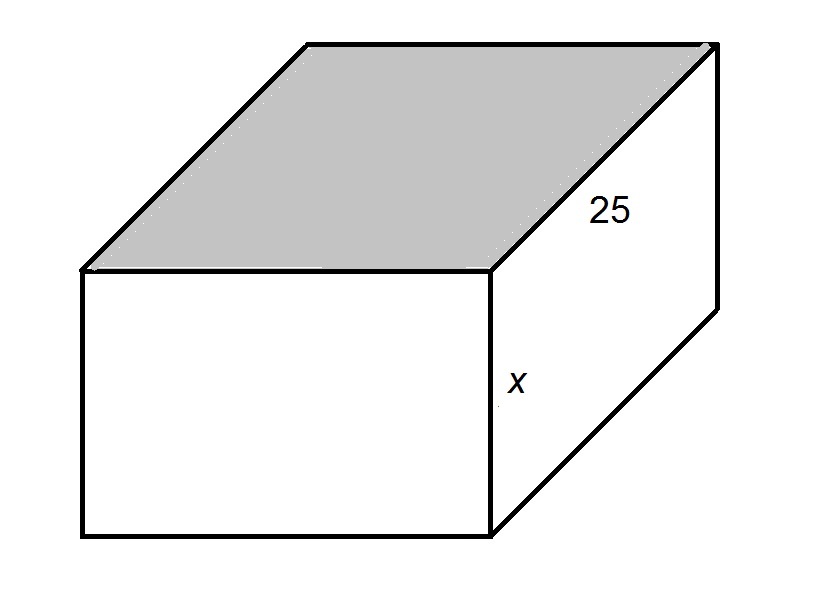
The shaded face of the provided rectangular prism is a square. If the surface area of the prism is , give in terms of .

Possible Answers:

$x = \frac{-25+\sqrt{4A+625}}{4}$

$x = \frac{A}{625}$

$x=\frac{ A - 1,250}{100}$

$x = \frac{-50+\sqrt{2A+2,500}}{2}$

$x=\frac{ A -2,500}{50}$

Correct answer:

$x=\frac{ A - 1,250}{100}$

Explanation:

Since the top face of the prism is a square, the common sidelength - and the missing dimension - is 25.

The surface area 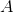of a rectangular prism with length , width , and height can be found using the formula

2LW + 2 WH + 2LH = A .

Setting H= x, L=W= 25 , and solving for :

$2 \cdot 25 \cdot 25 + 2 \cdot 25 \cdot x + 2 \cdot 25 \cdot x = A$

1,250 + 50x + 50 x = A

100 x + 1,250 = A

100 x + 1,250 - 1,250 = A - 1,250

100 x = A - 1,250

$\frac{100 x }{100}=\frac{ A - 1,250}{100}$

$x=\frac{ A - 1,250}{100}$

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Reuben
Certified Tutor

University of Alberta, Bachelor of Science, Mathematics.

View SAT Subject Test in Mathematics Level 1 Tutors

Peter
Certified Tutor

Nottingham University UK, Bachelor in Arts, Mathematics.

View SAT Subject Test in Mathematics Level 1 Tutors

Maggie
Certified Tutor

New York University, Bachelor of Science, Digital Communications and Multimedia.

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in San Diego, Computer Science Tutors in Houston, Statistics Tutors in Philadelphia, French Tutors in Atlanta, Algebra Tutors in San Francisco-Bay Area, SAT Tutors in Phoenix, Math Tutors in Denver, MCAT Tutors in Houston, Calculus Tutors in Atlanta, LSAT Tutors in Denver

Popular Courses & Classes

Spanish Courses & Classes in Los Angeles, ISEE Courses & Classes in Seattle, Spanish Courses & Classes in Chicago, GRE Courses & Classes in Phoenix, ISEE Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in San Diego, GRE Courses & Classes in Denver, SAT Courses & Classes in Miami, ACT Courses & Classes in Los Angeles, MCAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

LSAT Test Prep in San Diego, ACT Test Prep in Chicago, MCAT Test Prep in Houston, ISEE Test Prep in Atlanta, LSAT Test Prep in Chicago, MCAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Phoenix, ISEE Test Prep in Boston, ISEE Test Prep in Dallas Fort Worth, ISEE Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : Surface Area

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #771 : Geometry

Example Question #2 : How To Find The Surface Area Of A Cone

Example Question #16 : Solid Geometry

Example Question #123 : Geometry

Example Question #2 : How To Find The Surface Area Of A Cone

Example Question #21 : Surface Area

Example Question #22 : Surface Area

Example Question #27 : Surface Area

Example Question #28 : Surface Area

The surface area of the box is 82yd²(remember that area measurements are square units NOT cubic units)

Example Question #29 : Surface Area

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback:

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : Surface Area

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #771 : Geometry

Example Question #2 : How To Find The Surface Area Of A Cone

Example Question #16 : Solid Geometry

Example Question #123 : Geometry

Example Question #2 : How To Find The Surface Area Of A Cone

Example Question #21 : Surface Area

Example Question #22 : Surface Area

Example Question #27 : Surface Area

Example Question #28 : Surface Area

The surface area of the box is 82yd2 (remember that area measurements are square units NOT cubic units)

Example Question #29 : Surface Area

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

The surface area of the box is 82yd²(remember that area measurements are square units NOT cubic units)