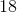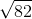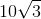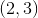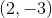Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : SAT Subject Test in Math I

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #12 : Transformation

What would f(x)=5x^3-7x^2+10x-61 become if it was reflected over the y-axis to become g(x) ?

Possible Answers:

g(x)=5x^3+7x^2+10x+61

g(x)=-5x^3+7x^2-10x+61

g(x)=-5x^3-7x^2-10x-61

g(x)=10x^3-14x^2+20x-61

g(x)=10x^2-14x^3-20x

Correct answer:

g(x)=-5x^3-7x^2-10x-61

Explanation:

When a function is reflected over the y-axis, g(x)=f(-x) .

f(x)=5x^3-7x^2+10x-61

becomes

g(x)=5(-x)(-x)(-x)-7(-x)(-x)+10(-x)-61

which is simplifed as

g(x)=-5x^3-7x^2-10x-61 .

Report an Error

Example Question #3 : Transformation

Let f(x) = x³ – 2x² + x +4. If g(x) is obtained by reflecting f(x) across the y-axis, then which of the following is equal to g(x)?

Possible Answers:

x³ + 2x² + x + 4

–x³ + 2x² – x + 4

–x³ – 2x² – x + 4

–x³ – 2x² – x – 4

x³ – 2x² – x + 4

Correct answer:

–x³ – 2x² – x + 4

Explanation:

In order to reflect a function across the y-axis, all of the x-coordinates of every point on that function must be multiplied by negative one. However, the y-values of each point on the function will not change. Thus, we can represent the reflection of f(x) across the y-axis as f(-x). The figure below shows a generic function (not f(x) given in the problem) that has been reflected across the y-axis, in order to offer a better visual understanding.

Therefore, g(x) = f(–x).

f(x) = x³ – 2x² + x – 4

g(x) = f(–x) = (–x)³ – 2(–x)² + (–x) + 4

g(x) = (–1)³x³ –2(–1)²x² – x + 4

g(x) = –x³ –2x² –x + 4.

The answer is –x³ –2x² –x + 4.

Report an Error

Example Question #3 : Transformation

What is the period of the function?

Screen_shot_2013-07-16_at_10.04.45_am

Possible Answers:

3π

2π

4π

Correct answer:

4π

Explanation:

The period is the time it takes for the graph to complete one cycle.

In this particular case we have a sine curve that starts at 0 and completes one cycle when it reaches $4\pi$ .

Therefore, the period is $4\pi$

Report an Error

Example Question #22 : How To Find Transformation For An Analytic Geometry Equation

Assume we have a triangle, $\bigtriangleup ABC$ , with the following vertices:

(4,6) , (2,9) , and (5,10)

If $\bigtriangleup ABC$ were reflected across the line y=x , what would be the coordinates of the new vertices?

Possible Answers:

$(-6,-4),\ (-9,-2),\ \textup{and } (-10, -5)$

$(-4, 6),\ (-2, 9),\ \textup{and } (-5, 10)$

$(6, -4),\ (9, -2),\ \textup{and } (10, -5)$

$(6,4),\ (9,2),\ \textup{and } (10,5)$

$(4, -6),\ (2, -9),\ \textup{and }(5, -10)$

Correct answer:

$(6,4),\ (9,2),\ \textup{and } (10,5)$

Explanation:

When we reflect a point across the line, y=x , we swap the x- and y-coordinates; therefore, in each point, we will switch the x and y-coordinates:

(4,6) becomes (6,4) ,

(2,9) becomes (9,2) , and

(5, 10) becomes (10,5) .

The correct answer is the following:

$(6,4),\ (9,2),\ \textup{and } (10,5)$

The other answer choices are incorrect because we only use the negatives of the coordinate points if we are flipping across either the x- or y-axis.

Report an Error

Example Question #1 : Distance Formula

Find the distance between (3, 4) and (-12, -5) .

Possible Answers:

$3 \sqrt {34}$

$2 \sqrt {6}$

$\sqrt {82}$

$10 \sqrt {3}$

Correct answer:

$3 \sqrt {34}$

Explanation:

For this problem we will need to use the distance formula:

$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

In our case,

(x_1,y_1)=(-12, -5) and (x_2,y_2)=(3, 4) .

Plugging these values into the formula we are able to find the distance.

$d = \sqrt {(3-(-12))^2 + (4-(-5)))^2))}$

$=\sqrt {15^2+9^2}$

$= \sqrt {306}$

$= \sqrt {9 \cdot 34} = 3 \sqrt {34}$

Report an Error

Example Question #2 : Distance Formula

What is the distance between (1,6) and (-3,-2) ?

Possible Answers:

$4\sqrt2$

$\frac{4}{3}$

$2\sqrt5$

$5\sqrt4$

$4\sqrt5$

Correct answer:

$4\sqrt5$

Explanation:

Write the distance formula.

$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Substitute the points:

(x_1,y_1)=(1,6)

(x_2,y_2)=(-3,-2)

$d=\sqrt{(-3-1)^2+(-2-6)^2}$

$d=\sqrt{16+64} = \sqrt{80}$

The radical can be broken down into factors of perfect squares.

$\sqrt{80} = \sqrt{16}\cdot \sqrt5 = 4\sqrt5$

The answer is: $4\sqrt5$

Report an Error

Example Question #1 : Midpoint Formula

Find the midpoint of the line that passes through the points (-1,4) and (5,2) .

Possible Answers:

(2,-3)

(3,3)

(2,3)

(3,-2)

(-3,2)

Correct answer:

(2,3)

Explanation:

Recall the midpoint formula as $(\frac{x1+x2}{2}, \frac{y1+y2}{2})$ .

Thus,

$(\frac{-1+5}{2},\frac{4+2}{2}) = (2,3)$

Report an Error

Example Question #1 : Midpoint Formula

Find the midpoint of the line that passes through the points (2,-1) and (-2,1) .

Possible Answers:

(2,1)

(2,-1)

(-2,1)

(0,0)

(-2,-1)

Correct answer:

(0,0)

Explanation:

Recall the midpoint formula as $(\frac{x1+x2}{2}, \frac{y1+y2}{2})$ .

Thus,

$(\frac{2+(-2)}{2},\frac{-1+1}{2}) = (0,0)$

Report an Error

Example Question #2 : Midpoint Formula

What is the midpoint between $\left ( 2,3\right )$ and $\left ( -7,4\right )$ ?

Possible Answers:

(-5,-7)

$\left(\frac{-5}{2}, \frac{7}{2}\right)$

(7,5)

(-5,7)

Correct answer:

$\left(\frac{-5}{2}, \frac{7}{2}\right)$

Explanation:

The formula to find the midpoint is as follows:

$\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)$

In our case our (x_1, y_1)= (2, 3)

our (x_2, y_2)=(-7, 4)

substituting in these values we get

midpoint = $\left(\frac{2+-7}{2}, \frac{3+4}{2}\right)=\left(\frac{-5}{2}, \frac{7}{2}\right)$

Report an Error

Example Question #4 : Midpoint Formula

What is the midpoint between $\left ( 1,3\right )$ and $\left ( 5,9\right )$ ?

Possible Answers:

$\left ( 1,5\right )$

$\left ( 1,9\right )$

$\left ( 3,9\right )$

$\left ( 3,5\right )$

$\left ( 3,6\right )$

Correct answer:

$\left ( 3,6\right )$

Explanation:

To find the midpoint of two points you find the average of both the values and values.

For ,

$\frac{1+5}{2}=3$ .

For ,

$\frac{3+9}{2}=6$ .

This means the midpoint is $\left ( 3,6\right )$ .

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View SAT Subject Test in Mathematics Level 1 Tutors

Reuben
Certified Tutor

University of Alberta, Bachelor of Science, Mathematics.

View SAT Subject Test in Mathematics Level 1 Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Washington DC, GRE Tutors in San Diego, Chemistry Tutors in Atlanta, LSAT Tutors in Phoenix, Physics Tutors in Dallas Fort Worth, Statistics Tutors in Dallas Fort Worth, English Tutors in Philadelphia, Calculus Tutors in New York City, MCAT Tutors in Seattle, SAT Tutors in Atlanta

Popular Courses & Classes

GRE Courses & Classes in Houston, GRE Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Atlanta, ACT Courses & Classes in Boston, GMAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in New York City, SAT Courses & Classes in Washington DC, MCAT Courses & Classes in Los Angeles, SAT Courses & Classes in Chicago, SSAT Courses & Classes in San Diego

Popular Test Prep

ACT Test Prep in Boston, LSAT Test Prep in Phoenix, LSAT Test Prep in Los Angeles, GMAT Test Prep in Philadelphia, SSAT Test Prep in Seattle, ISEE Test Prep in Seattle, GMAT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Atlanta, LSAT Test Prep in New York City, ISEE Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : SAT Subject Test in Math I

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #12 : Transformation

Example Question #3 : Transformation

Example Question #3 : Transformation

Example Question #22 : How To Find Transformation For An Analytic Geometry Equation

Example Question #1 : Distance Formula

Example Question #2 : Distance Formula

Example Question #1 : Midpoint Formula

Example Question #1 : Midpoint Formula

Example Question #2 : Midpoint Formula

Example Question #4 : Midpoint Formula

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: