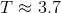The first number is multiplied by three 

.  

Then it is divide by two 

.  

The following is multiplied by three 

then divided by two 

.  

That makes the next step to multiply by three which gives us 

.

Rewrite the first term in fraction form: .

The sequence now begins 

,...

Rewrite the terms with their least common denominator, which is :

The common difference  of the sequence is the difference of the second and first terms, which is

.

The rule for term  of an arithmetic sequence, given first term  and common difference , is 

;

Setting , , and  , we can find the tenth term  by evaluating the expression:

,

the correct response.

Using the Product of Radicals principle, we can simplify the first two terms of the sequence as follows:

The common ratio  of a geometric sequence is the quotient of the second term and the first:

Multiply the second term by the common ratio to obtain the third term:

The common ratio  of a geometric sequence is the quotient of the third term and the second:

Multiplying numerator and denominator by , this becomes

The second term of the sequence is equal to the first term multiplied by the common ratio:

.

so equivalently:

Substituting:

,

the correct response.

The common ratio  of a geometric sequence is the quotient of the second term and the first:

Simplify this common ratio by multiplying both numerator and denominator by :

Multiply the second term by the common ratio to obtain the third term:

Let  be the common ratio of the geometric sequence. Then 

and 

Therefore, 

,

and

Setting :

.

Substituting for  and , either

.

The second term can be either  or , the former of which is a choice.

Let  be the common ratio of the geometric sequence. Then 

and 

Therefore, 

,

Setting , and applying the Quotient of Radicals Rule:

Taking the square root of both sides:

Substituting, and applying the Product of Radicals Rule:

Since all elements of the sequence are positive, .

In modulo 6 arithmetic, a number is congruent to the reainder of its division by 6.

Therefore, since  and ,

.

The correct response is 0.

A set is closed under addition if and only if the sum of any two (not necessarily distinct) elements of the set is also an element of the set.

 is closed under addition, since 

The set of all negative integers is closed under addition, since any two negative integers can be added to yield a third negative integer.

The set of all positive even integers is closed under addition, since any two positive even integers can be added to yield a third positive even integer.

The remaining set is the set of all integers between 1 and 10 inclusive. It is not closed under addition, as can be seen by this counterexample:

but 

 varies directly as , which means that for some constant of variation ,

We can write this relationship alternatively as

where the initial conditions can be substituted on the left side and final conditions, on the right. We will be solving for  in the equation